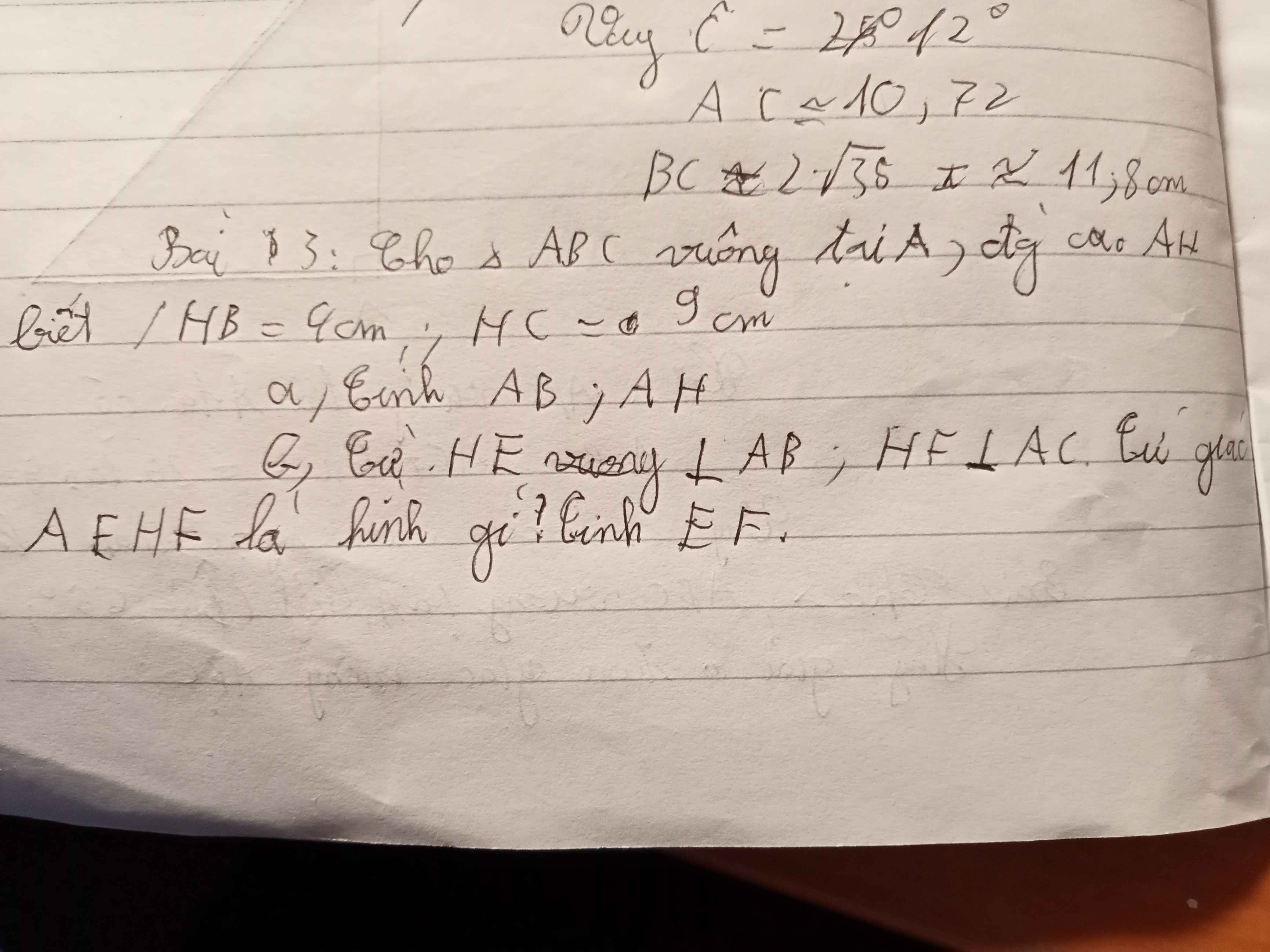a) Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB(gt)
nên \(AE\cdot AB=AH^2\)(định lí 1 về hệ thức lượng trong tam giác vuông)(1)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC(gt)
nên \(AF\cdot AC=AH^2\)(định lí 1 về hệ thức lượng trong tam giác vuông)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)(đpcm)
b) Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB(gt)
nên \(HE^2=AE\cdot EB\)(định lí 2 về hệ thức lượng trong tam giác vuông)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC(gt)
nên \(HF^2=AF\cdot FC\)(định lí 2 về hệ thức lượng trong tam giác vuông)
Ta có: \(AE\cdot EB+AF\cdot FC=HE^2+HF^2\)(3)
Xét tứ giác AEHF có:
\(\widehat{FAE}=90^0\)(\(\widehat{CAB}=90^0\), F∈AC, E∈AB)
\(\widehat{HEA}=90^0\)(HE⊥AB)
\(\widehat{HFA}=90^0\)(HF⊥AC)
Do đó: AEHF là hình chữ nhật(dấu hiệu nhận biết hình chữ nhật)
⇒\(\widehat{EHF}=90^0\)
Áp dụng định lí pytago vào ΔEHF vuông tại H, ta được:
\(EF^2=HE^2+HF^2\)(4)
Từ (3) và (4) suy ra \(AE\cdot EB+AF\cdot FC=EF^2\)(5)
Ta có: AEHF là hình chữ nhật(cmt)
⇒AH=EF(hai đường chéo trong hình chữ nhật AEHF)
⇒\(AH^2=EF^2\)(6)
Từ (5) và (6) suy ra \(AE\cdot EB+AF\cdot FC=AH^2\)(cmt)