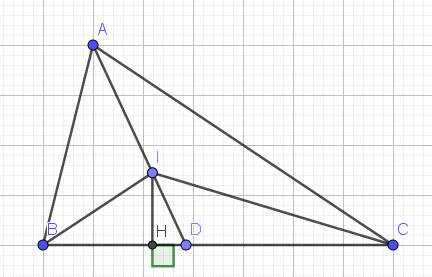
Lời giải:
Ta thấy:
$\widehat{BID}=180^0-\widehat{BIA}=\widehat{ABI}+\widehat{BAI}$
$=\frac{\widehat{B}}{2}+\frac{\widehat{A}}{2}=\frac{\widehat{A}+\widehat{B}}{2}$
$=\frac{180^0-\widehat{C}}{2}=90^0-\widehat{C}.\frac{1}{2}$
$=90^0-\widehat{ICH}=\widehat{CIH}$
Vậy:
$\widehat{BID}=\widehat{CIH}$
$\Rightarrow \widehat{BIH}+\widehat{HID}=\widehat{HID}+\widehat{CID}$
$\Rightarrow \widehat{BIH}=\widehat{CID}$ (đpcm)