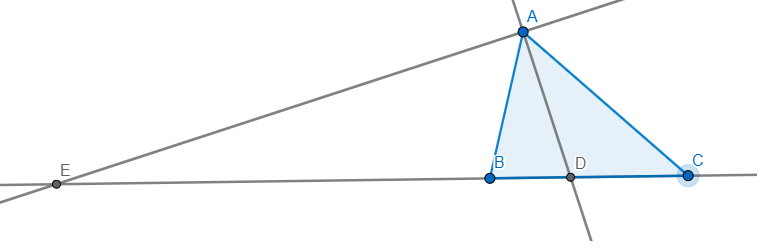
tia phân giác trong góc A cắt BC tại D
Vì AD,AE lần lượt là phân giác trong và ngoài của góc A \(\Rightarrow AD\bot AE\Rightarrow\angle EAB=90-\angle BAD=90-\dfrac{1}{2}\angle BAC\)
Ta có: \(\angle AEB=\angle ABC-\angle EAB=\angle ABC-90+\dfrac{1}{2}\angle BAC\)
\(=\angle ABC-90+\dfrac{1}{2}\left(180-\angle ABC-\angle ACB\right)\)
\(=\angle ABC-90+90-\dfrac{1}{2}\angle ABC-\dfrac{1}{2}\angle ACB=\dfrac{1}{2}ABC-\dfrac{1}{2}\angle ACB\)
Ta có: \(\widehat{BAD}\) là góc ngoài tại đỉnh A của ΔABC(gt)
nên \(\widehat{BAD}=\widehat{ABC}+\widehat{ACB}\)
\(\Leftrightarrow\widehat{EAB}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\)
Ta có: \(\widehat{ABE}\) là góc ngoài tại đỉnh B của ΔABC(gt)
nên \(\widehat{ABE}=\widehat{BAC}+\widehat{ACB}\)
\(\Leftrightarrow\widehat{ABE}=180^0-\widehat{BAD}+\widehat{ACB}\)
\(\Leftrightarrow\widehat{ABE}=180^0-\widehat{ABC}-\widehat{ACB}+\widehat{ACB}\)
\(\Leftrightarrow\widehat{ABE}=180^0-\widehat{ABC}\)
Xét ΔEBA có
\(\widehat{AEB}+\widehat{EAB}+\widehat{ABE}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{AEB}=180^0-180^0+\widehat{ABC}-\dfrac{1}{2}\widehat{ABC}-\dfrac{1}{2}\widehat{ACB}\)
\(\Leftrightarrow\widehat{AEB}=\dfrac{1}{2}\widehat{ABC}-\dfrac{1}{2}\widehat{ACB}\)















