Question

Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD ở I, cắt AC ở K

a) Chứng minh rằng AK = KC, BI = ID

b) Cho AB = 6cm, CD = 10 cm. Tính các độ dài EI, KF, IK ?

Answer 1

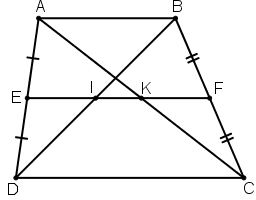
a) Vì EA = ED, FB = FC (gt)

Nên EF là đường trung bình của hình thang ABCD.

Do đó: EF // AB // CD

∆ABC có BF = FC và FK // AB

nên: AK = KC

∆ABD có AE = ED và EI // AB

nên: BI = ID

b) Vi EF là đường trung bình của hình thang ABCD.

nên EF = = \(\dfrac{6+10}{2}=8\)

EI là đường trung bình của ∆ABD nên \(EI=\dfrac{1}{2}AB=\dfrac{1}{2}.6=3\left(cm\right)\)

KF là đường trung bình của ∆ABC nên \(KF=\dfrac{1}{2}AB=\dfrac{1}{2}.6=3\left(cm\right)\)

Lại có EF = EI + IK + KF

nên IK = EF - (EI + KF) = 8 - (3 + 3) = 2 (cm)

Answer 2

a) + Hình thang ABCD có EA = ED, FB = FC (gt)

⇒ EF là đường trung bình của hình thang ABCD.

⇒ EF // AB // CD

+ ΔABC có BF = FC (gt) và FK // AB (cmt)

⇒ AK = KC

+ ΔABD có: AE = ED (gt) và EI // AB (cmt)

⇒ BI = ID

b) + Vì EF là đường trung bình của hình thang ABCD.

⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.

+ ΔABD có AE = ED, DI = IB

⇒ EI là đường trung bình của ΔABD

⇒ EI = AB/2 = 6/2 = 3(cm)

+ ΔABC có CF = BF, CK = AK

⇒ KF là đường trung bình của ΔABC

⇒ KF = AB /2 = 6/2 = 3cm

+ Lại có: EI + IK + KF = EF

⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm