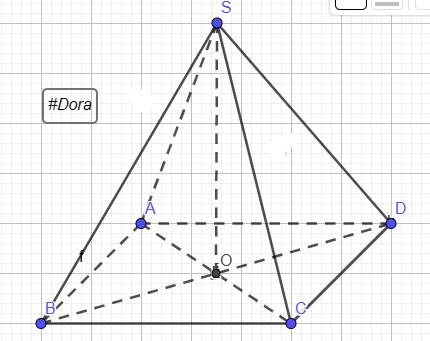
Vì `SA=SC; SB=SD`
Mà `O` là trung điểm `AC;BD`
`=>SO \bot AC; SO \bot BD`
`=>SO \bot (ABCD)`
Vì `OC \bot BD; OC \bot SO =>OC \bot (SBD)`
`=>(SC,(SBD))=\hat{OSC}=30^o`
Ta có: `OC=1/2 AC=\sqrt{2}/2 a`
`=>SO=[OC]/[tan \hat{OSC}]=\sqrt{6}/2 a`
`=>V_[S.ABCD]=1/3 . \sqrt{6}/2 a .a^2 = \sqrt{6}/6 a^3`.












