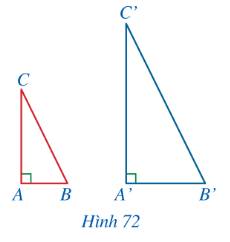
Ta có: \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)
Hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ nên \(\widehat {A'} = \widehat A = 90^\circ \).
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat {A'} = \widehat A\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c)
\( \Rightarrow \widehat B = \widehat {B'}\).