Ôn tập chương II - Đa giác. Diện tích đa giác
Các câu hỏi tương tự
Cho hình vuông ABCD trên cạnh BC lấy điểm M sao cho BM = \(\dfrac{BC}{3}\), trên tia đối của tia CD lấy N sao cho CN= \(\dfrac{AD}{2}\) I là giao điểm của tia AM và BN Chứng minh rằng 5 điểm A, B, I, C, D cũng cách đều 1 điểm
HELP :<
Cho hình bs.31
(R là điểm bất kì trên QP. S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng :
(A) dfrac{1}{2}S (B) dfrac{1}{4}S
(C) dfrac{3}{4}S (D) S
Hãy lựa chọn phương án đúng ?
Đọc tiếp
Cho hình bs.31
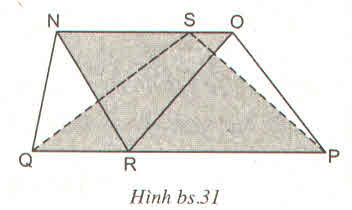
(R là điểm bất kì trên QP. S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng :
(A) \(\dfrac{1}{2}S\) (B) \(\dfrac{1}{4}S\)
(C) \(\dfrac{3}{4}S\) (D) \(S\)
Hãy lựa chọn phương án đúng ?
Cho hình vuông ABCD, trên cạnh AB, BC, CD, DA lấy các điểm M, N, E, F sao cho AM = CN = CE = AF. a) Chứng minh tứ giác ANCF là hình bình hành b) Chứng minh MNEF là hình chữ nhật c) Gọi H là hình chiếu của A trên BF. Tính góc CHM (gợi ý câu c chứng minh góc CHB= góc AHM)
1/ a. Chứng minh công thức Hê-rông tính diện tích tam giác theo 3 cạnh a,b,c Ssqrt{pleft(p-aright)left(p-bright)left(p-cright)} (p là nửa chu vi)
b. Áp dụng chứng minh rằng nếu Sdfrac{1}{4}left(a+b-cright)left(a+c-bright) thì tam giác đó là tam giác vuông
2/ Cho tứ giác ABCD. Lấy M,Nin AB sao cho AMMNNB. Lấy E,Fin BC sao cho BEEFFC. Lấy P,Qin CD sao cho CPPQQD. Lấy G,Hin AD sao cho DGGHHA. Gọi A,B là giao điểm của MQ và NP với EH, C,D là giao điểm của MQ và NP với FG. Chứng minh rằng
a. S_{...
Đọc tiếp
1/ a. Chứng minh công thức Hê-rông tính diện tích tam giác theo 3 cạnh a,b,c S=\(\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là nửa chu vi)
b. Áp dụng chứng minh rằng nếu \(S=\dfrac{1}{4}\left(a+b-c\right)\left(a+c-b\right)\) thì tam giác đó là tam giác vuông
2/ Cho tứ giác ABCD. Lấy \(M,N\in AB\) sao cho AM=MN=NB. Lấy \(E,F\in BC\) sao cho BE=EF=FC. Lấy \(P,Q\in CD\) sao cho CP=PQ=QD. Lấy \(G,H\in AD\) sao cho DG=GH=HA. Gọi A',B' là giao điểm của MQ và NP với EH, C',D' là giao điểm của MQ và NP với FG. Chứng minh rằng
a. \(S_{MNPQ}=\dfrac{1}{3}S_{ABCD}\) b. \(S_{A'B'C'D'}=\dfrac{1}{9}S_{ABCD}\)
3/ Lấy M tùy ý nằm trong tam giác ABC. Gọi D,E,F là hình chiếu của M trên BC,AC,AB. Đặt BC=a,AC=b,AB=c,MD=x,ME=y,MF=z. Chứng minh rằng
a. ax+by+cz=2S (S=Sabc)
b. \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}\ge\dfrac{2p^2}{S}\) (\(p=\dfrac{a+b+c}{2}\) )
Cho tam giác DEF vuông tại D,N là một điểm bất kì trên EF. Gọi H và K lần lượt là hình chiếu của N lên DE,DF
a)chứng minh tứ giác DHNK là hình chữ nhật
b) Nếu N là trung điểm của EF và DN = 12,5 cm thì EF dài bao nhiêu?
c) Tìm vị trí của điểm N trên EF để KH có độ dài nhỏ nhất?
Xem chi tiết
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo.Trên đoạn thẳng OB lấy điểm E sao cho OE>BE.Gọi F là điểm đối xứng với C qua E.Chứng minh OE=1/2 AF
Trong tam giác vuông ABC (∠C = 90◦ ), các điểm K, L và M lần lượt nằm trên các cạnh AC, BC và AB sao cho AK = BL = a, KM = LM = b và ∠KML = 90◦ . Chứng minh rằng a = b
Cho tam giác ABC vuông tại A và đường trung tuyến AM (M∈BC)(M∈BC). Từ điểm P trên cạnh AB (P khác A và B), vẽ đường thẳng song song với BC và AM, hai đường thẳng này cắt AM và BC lần lượt tại N và K.
a/Chứng minh rằng tứ giác PNMK là hình bình hành
b/Trên tia đối của tia MA lấy điểm D sao cho MD MA. Chứng minh rằng ABCD là hình chữ nhật
c/Chứng minh rằng PK + PN dfrac{AD}{2}
d/Xác định vị trí của điểm P trên cạnh AB để tứ giác PNMK là hình thoi
e/Tìm điều kiện để tứ giác PNMK là hình vuôn...
Đọc tiếp
Cho tam giác ABC vuông tại A và đường trung tuyến AM (M∈BC)(M∈BC). Từ điểm P trên cạnh AB (P khác A và B), vẽ đường thẳng song song với BC và AM, hai đường thẳng này cắt AM và BC lần lượt tại N và K.
a/Chứng minh rằng tứ giác PNMK là hình bình hành
b/Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh rằng ABCD là hình chữ nhật
c/Chứng minh rằng PK + PN = \(\dfrac{AD}{2}\)
d/Xác định vị trí của điểm P trên cạnh AB để tứ giác PNMK là hình thoi
e/Tìm điều kiện để tứ giác PNMK là hình vuông
Cho tứ giác ABCD. Hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G và H lần lượt là trung điểm của các cạnh AB, BC, CD và DA
a) chứng minh tứ giác EFGH là hình chữ nhật
b) biết AC=10cm, BD=8cm. Tính diện tích tứ giác EFGH
c) Để EFGH là hình vuông thì tứ giác ABCD cần có thêm điều kiện gì về hai đường chéo ?
Xem chi tiết











