* Phương án đúng:
(D). S
* Giải thích:
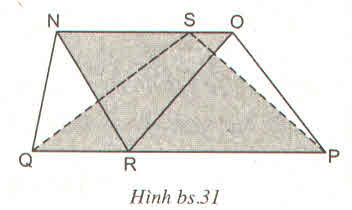
Đường cao của hình thang cũng chính bằng độ dài đường cao của hai tam giác QSP và NRO.
Gọi độ dài đường cao là h (h>0)
SQSP= \(\dfrac{1}{2}.h.QP\)
SNRO= \(\dfrac{1}{2}.h.NO\)
SNRO+SQSP=\(\dfrac{1}{2}.h.NO\)+\(\dfrac{1}{2}.h.QP\)= \(\dfrac{1}{2}.h.\left(NO+QP\right)\) (1)
Ta có:
SNOPQ=S=\(\left(NO+QP\right).h.\dfrac{1}{2}\) (2)
Từ (1) và (2) => SNRO+SQSP=S=\(\dfrac{1}{2}.h.\left(NO+QP\right)\)