* Phương án đúng:
Quan hệ đúng của diện tích 3 hình vuông là:
(A). \(S_3+S_2=S_1\)
* Phương án đúng:
Quan hệ đúng của diện tích 3 hình vuông là:
(A). \(S_3+S_2=S_1\)
Cho hình bs.31
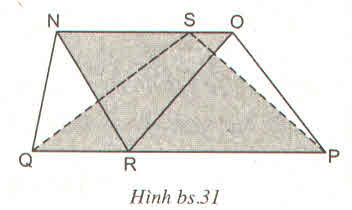
(R là điểm bất kì trên QP. S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng :
(A) \(\dfrac{1}{2}S\) (B) \(\dfrac{1}{4}S\)
(C) \(\dfrac{3}{4}S\) (D) \(S\)
Hãy lựa chọn phương án đúng ?
Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng :
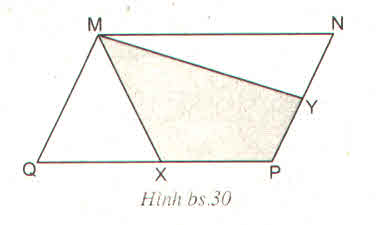
(A) \(\dfrac{1}{4}S\) (B) \(\dfrac{1}{2}S\)
(C) \(\dfrac{1}{8}S\) (D) \(\dfrac{3}{4}S\)
Chọn phương án đúng ?
Cho hình bs.29, trong đó HK = KF = FL = LT và tam giác GHT có diện tích S. Khi đó, diện tích của tam giác GKL bằng :
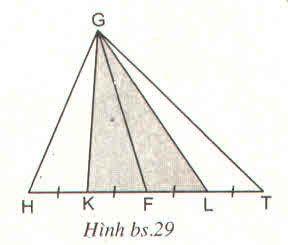
(A) \(\dfrac{1}{2}S\) (B) \(\dfrac{1}{4}S\)
(C) \(\dfrac{1}{8}S\) (D) \(\dfrac{3}{4}S\)
Chọn phương án đúng ?
Cho lục giác đều MNPQRS (h.bs.27). Gọi A, Y, Z tương ứng là trung điểm các cạnh MN, PQ và RS. Khi đó XYZ là :
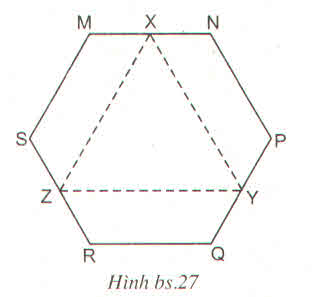
(A) Tam giác vuông
(B) Tam giác vuông cân
(C) Tam giác đều
(D) Tam giác mà độ dài các cạnh của nó đôi một khác nhau
Hãy chọn phương án đúng ?
Cho tam giác MNP. Điểm T nằm trong tam giác MNP sao cho các tam giác TMN, TMP, TPN có diện tích bằng nhau. Khi đó, T là giao điểm
(A) ba đường cao của tam giác đó
(B) ba đường trung trực của tam giác đó
(C) ba đường trung tuyến của tam giác đó
(D) ba đường phân giác trong của tam giác đó
Hãy lựa chọn phương án đúng ?
Cho ΔABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I.
a) CMR: AD song2 BM và tứ giác ADBM là hình tho.
b) Gọi E là giao điểm của AM và AD. C/m: AE = EM.
c) Cho BC = 5cm và AC = 4cm. Tính S Δ ABM.
Cho tam giác MNP vuông tại M,đường cao AH,kẻ HD vuông góc MN(B thuộc MN),HE vuông góc MP (E thuộc MP)
a)Chứng mình MDHE là hình chữ nhật
b)Gọi A là trung điểm của HP.Chứng mình tam giác DEA vuông
c) tam giác MNP có thêm điều kiện gì để DE=2AE
Cho tam giác MNP vuông tại M,đường cao AH,kẻ HD vuông góc MN(B thuộc MN),HE vuông góc MP (E thuộc MP)
a)Chứng mình MDHE là hình chữ nhật
b)Gọi A là trung điểm của HP.Chứng mình tam giác DEA vuông
c) tam giác MNP có thêm điều kiện gì để DE=2AE
Cho hình bình hành MNPQ có MN = 2MQ và ∠M = 120o. Gọi I, K lần lượt là trung điểm của MN và PQ; A là điểm đối xứng của Q qua M.
a) Tứ giác MIKQ là hình gì? Vì sao?
b) C/m: ΔAMI là Δ đều.
c) C/m: tứ giác AMPN là hcn.
d) Cho AI = 4cm. Tính S của hcn AMPN.