Cho góc nhọn xOy. Gọi M là một điểm thuộc tia phân giác của góc xOy, kẻ MA vuông góc Ox (A thuộc Ox) ; kẻ MB vuông góc Oy (B thuộc Oy).
a) Chứng minh tam giác OAB cân tại B
b) Đường thẳng BM cắt Ox tại D, đường thẳng AM cắt Oy tại E. Chứng minh rằng: MD = ME
c) Chứng minh: OM vuông góc DE
GIÚP MÌNH VỚI MÌNH SẮP THI RỒI !!!!
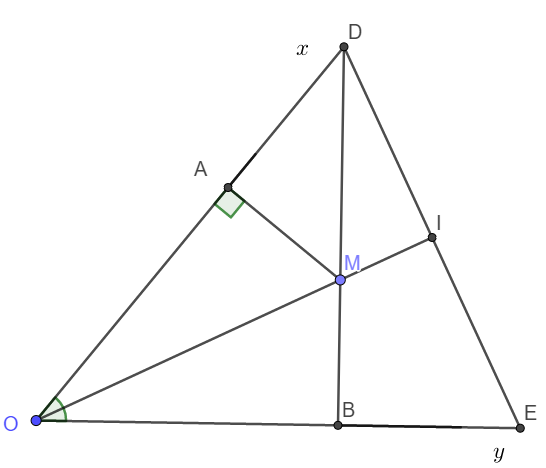
a) Xét tam giác vuông AOM và tam giác vuông BOM , ta có :
Cạnh hyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) ( cạnh huyền - góc nhọn )
\(\Rightarrow MA=MB;OA=AB\) hay \(\Delta OAB\) cân tại O
b) Xét tam giác vuông AMD và tam giác vuông BME , ta có :
AM = BM
\(\widehat{AMD}=\widehat{BME}\) ( hai góc đối đỉnh )
\(\Rightarrow\Delta AMD=\Delta BME\) ( cạnh góc vuông - góc nhọn kề )
=> MD = ME
c) Ta thây OA = OB ; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\) (c.g.c)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.
a.Xét tam giác OAM vuông tại A (MA vuông góc với Ox) và tam giác OBM vuông tại B (MB vuông góc với Oy) có:
Góc OAM= góc BOM (M thuộc tia phân giác góc O)
Chung cạnh huyền OM
=> Tam giác OAM=tam giác OBM (cạnh huyền-góc nhọn)
=> OA=OB (hai cạnh tương ứng)
=> Tam giác OAB cân tại O (có 2 cạnh bằng nhau)
b. Ta có:
Góc OAM+ góc DAM= 180 độ (hai góc kề bù)
Góc OBM+góc EBM=180 độ (hai góc kề bù)
Mà Góc OAM=góc OBM (tam giác OAM=tam giác OBM)
=> Góc DAM= góc EBM
Xét tam giác ADM và tam giác BEM có:
Góc DAM= góc EBM (cmt)
MA=MB (tam giác OAM= tam giác OBM)
Góc AMD= góc BME (hai góc đối đỉnh)
=> Tam giác ADM= tam giác BEM ( g.c.g)
=>MD=ME (hai cạnh tương ứng)
c. Ta có : OA+BE= OE
OA+AD= OD
Mà OA=OB (c/m phần a)
BE=AD (tam giác ADM=tam giác BEM)
=> OE=OD
=> Tam giác OED cân tại O
Mà OM là đường phân giác góc O
=> OM cũng là đường cao của tam giác OED (t/c tâm giác cân)
=> OM vuông góc với DE
Phần c có thể c/m theo cách khác nhưng cách trên ngắn hơn
xét △AMO và △BMO có
\(\widehat{A}=\widehat{B}=90^0\)
OM chung
\(\widehat{O1}=\widehat{O2}\) (gt)
=> △AMO = △BMO (ch-gn)
=> OA=OB (2 cạnh tương ứng )
=> △OAB cân tại O (đpcm)
b) vì △AMO = △BMO (theo a)
=> MA=MB (2 cạnh tương ứng )
xét △MDA và △MEB có
\(\widehat{A}=\widehat{B}\)
MA=MB (cmt)
\(\widehat{AMO}=\widehat{BME}\) (ĐỐI ĐỈNH)
=> △MDA = △MEB (g.c.g)
=> MD=ME (2 cạnh tương ứng )(đpcm)
c)vì △MDA = △MEB (theo b)
=> AD=BE (2 cạnh tương ứng )
ta có
* OA=OB;DA=BE
=> OA+DA=OB+BE
=> OD=OE
=> △ ODE cân tại O
=> OM vừa là đường pg vừa là đường vuông góc
=> OM ⊥ED(đpcm)













