16 tháng 6 2022 lúc 21:08
Ôn thi vào 10
Các câu hỏi tương tự
Từ điểm A ở ngoài đường tròn tâm O, vẽ 2 tiếp tuyến AB và AC với (O) (B và C là các tiếp điểm). OA cắt BC tại H, cắt đường tròn (O) tại 2 điểm I và K (I thuộc cung BC nhỏ, K thuộc cung BC lớn). Vẽ đường kính CD, cát tuyến AD cắt (O) tại M. BM cắt OA tại NChứng minh: a) Tứ giác AMHC nội tiếp b) N là trung điểm của AH c) 1/AN1/AI+1/AK
Đọc tiếp
Từ điểm A ở ngoài đường tròn tâm O, vẽ 2 tiếp tuyến AB và AC với (O) (B và C là các tiếp điểm). OA cắt BC tại H, cắt đường tròn (O) tại 2 điểm I và K (I thuộc cung BC nhỏ, K thuộc cung BC lớn). Vẽ đường kính CD, cát tuyến AD cắt (O) tại M. BM cắt OA tại N
Chứng minh: a) Tứ giác AMHC nội tiếp
b) N là trung điểm của AH
c) 1/AN=1/AI+1/AK
Cho đường tròn (O;R) với dây CD cố định .Điểm M thuộc tia đối của tia DC.Qua M kẻ hai tiếp tuyến MA,MB tới đường tròn (O;R) (A thuộc cung lớn CD) . Gọi I là trung điểm của CD , OM cắt AB tại H.Tia OI cắt AB tại K ,nối AB cắt CD tại Ea) C/m 4 điểm M,H,I,K cùng thuộc 1 đường trònb) C/m ME.MIMA^2c) Xác định vị trí của M để tam giác MAB đềud) C/m KC là tiếp tuyến của đường tròn
Đọc tiếp
Cho đường tròn (O;R) với dây CD cố định .Điểm M thuộc tia đối của tia DC.Qua M kẻ hai tiếp tuyến MA,MB tới đường tròn (O;R) (A thuộc cung lớn CD) . Gọi I là trung điểm của CD , OM cắt AB tại H.Tia OI cắt AB tại K ,nối AB cắt CD tại E
a) C/m 4 điểm M,H,I,K cùng thuộc 1 đường tròn
b) C/m ME.MI=MA^2
c) Xác định vị trí của M để tam giác MAB đều
d) C/m KC là tiếp tuyến của đường tròn
Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn đó (C khác A , B ). Lấy điểm D thuộc dây BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F.
a. Chứng minh rằng FCDE là tứ giác nội tiếp đường tròn.
b. Chứng minh rằng DA.DE = DB.DC.
7 tháng 6 2021 lúc 8:27
cho tam giác ABC nhọn (ABAC) nội tiếp đường tròn đường O các đường cao BF và CK của tam giác cắt nhau tại H . Tia FK cắt tia CB tại M , AH cắt BC và đường tròn O lần lượt tại D và EA/chứng minh tứ giác BKFC nội tiếp và MKMF MBMC ( khúc này tui k hiểu đề nói j , có sai đề thì nhắc mình nha :3333)B/ AM cắt đường tròn O tại N (N khác A) . chứng minh góc AKN góc AFNthank :3333333333333
Đọc tiếp
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn đường O các đường cao BF và CK của tam giác cắt nhau tại H . Tia FK cắt tia CB tại M , AH cắt BC và đường tròn O lần lượt tại D và E
A/chứng minh tứ giác BKFC nội tiếp và MKMF =MBMC ( khúc này tui k hiểu đề nói j , có sai đề thì nhắc mình nha :3333)
B/ AM cắt đường tròn O tại N (N khác A) . chứng minh góc AKN = góc AFN
thank :3333333333333
Chon đường tròn O ,đường kính ab=2r .C là điểm bất kì trên đường tròn cắt đường thẳng BC tại I.Chứng minh tứ giác AOMI nội tiếp.Vẽ dây cung Ak vuông góc OI tại E .Chứng minh I k là tiếp tuyến của đường tròn o .Vẽ dây cung AD song song BC .Chứng minh ba điểm D,M,K thẳng hàng
Cho đường tròn (0) đường kính AB .trên cùng nửa mp bờ AB vẽ 2 tia tiếp tuyến Ax,By .M là điểm thuộc đường tròn sao cho tiếp tuyến tại M cắt Ax,By cắt nhau tại D và C C/m : AD +BC =CD, góc DOC =90°, đường kính CD tiếp xúc AB tại (o)
Cho đường tròn O có đường kính AB. Từ điểm S thuộc tia đối của tia AB kẻ hai tiếp tuyến SC và SD dây CD cắt AB tại H. Vẽ đường tròn (O) đi qua C và tiếp xúc với đường thẳng AB tại S. Hai đường tròn O và (O)cắt nhau tại điểm M khác C. a) Chứng minh tứ giác SMHD nội tiếp. b) Gọi K là hình chiếu vuông góc của C trên BD I, là giao điểm của BM và CK. Chứng minh HI song song với BD. c) Các đường thẳng SM và HM lần lượt cắt O tại các điểm L và T ( L T, khác M ). Chứng minh rằng tứ giác CDTL là...
Đọc tiếp
Cho đường tròn O có đường kính AB. Từ điểm S thuộc tia đối của tia AB kẻ hai tiếp tuyến SC và SD dây CD cắt AB tại H. Vẽ đường tròn (O') đi qua C và tiếp xúc với đường thẳng AB tại S. Hai đường tròn O và (O')cắt nhau tại điểm M khác C. a) Chứng minh tứ giác SMHD nội tiếp. b) Gọi K là hình chiếu vuông góc của C trên BD I, là giao điểm của BM và CK. Chứng minh HI song song với BD. c) Các đường thẳng SM và HM lần lượt cắt O tại các điểm L và T ( L T, khác M ). Chứng minh rằng tứ giác CDTL là hình vuông khi và chỉ khi 2 MC^2=MS.MD
Cho đường tròn (O; R) và dây MN không đi qua tâm O. Kẻ đường kính AB vuông góc với MN tại E. Lấy điểm C thuộc dây MN. BC cắt đường tròn (O;R) tại K. a) Chứng minh: Tứ giác AKCE nội tiếp b) Gọi I là giao điểm của AK và MN, D là giao điểm của AC và BI. Chứng minh C cách đều 3 cạnh của tam giác DEK
24 tháng 5 2022 lúc 11:16
Cho đg tròn `(O;R)` , dây `BC` khác đg kính . Qua `O` kẻ đường vuông góc với `BC` tại `I` , cắt tiếp tuyến tại `B` của đường tròn tại điểm `A` . Vẽ đường kính `BD`. Đường thẳng vuông góc với `BD` tại `O` cắt `BC` tại `K` . Chứng minh rằng :
`a)`\(CD//OA\)
`b)AC` tiếp tuyến của đường tròn `(O)`
`c)IK*IC+IO*IA=R^2`
14 tháng 5 2022 lúc 16:37
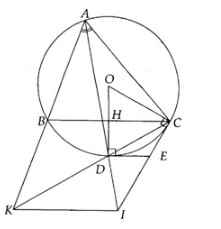
Cho đường tròn \(\left(O;AB=2R\right)\). Lấy C là một điểm trên đường tròn để \(AC>BC\). Vẽ hình vuông ACDE có D thuộc tia tia đối của tia BC. CE cắt đường tròn tại F (F không trùng C). Qua A, kẻ tiếp tuyến cắt BF tại H. Chứng minh rằng D, E, H thẳng hàng.
*Giải bằng cách xét 2 tam giác AEH và ACB