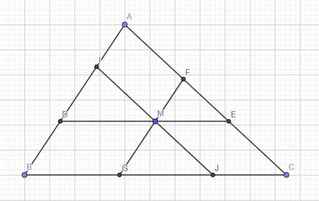
\(\left\{{}\begin{matrix}\widehat{MGJ}=\widehat{B}\left(\text{đồng vị}\right)\\\widehat{MJG}=\widehat{C}\left(\text{đồng vị}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MGJ\sim\Delta ABC\) theo tỉ số \(k_1=\dfrac{GJ}{BC}\)
\(\Rightarrow S_{ABC}.k_1^2=S_{MGJ}\Rightarrow k_1=\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}=\dfrac{GJ}{BC}\) (1)
Tương tự: \(\dfrac{DM}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\), mà BDMG là hbh (2 cặp cạnh đối song song)
\(\Rightarrow DM=BG\Rightarrow\dfrac{BG}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\) (2)
Tương tự: \(\dfrac{CJ}{BC}=\sqrt{\dfrac{S_{FME}}{S_{ABC}}}\) (3)
Cộng vế (1);(2);(3) \(\Rightarrow\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}+\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}+\sqrt{\dfrac{S_{FME}}{S_{ABC}}}=\dfrac{BG+GJ+JC}{BC}=1\)
\(\Rightarrow S_{ABC}=\left(\sqrt{S_{MGJ}}+\sqrt{S_{IDM}}+\sqrt{S_{FME}}\right)^2\le3\left(S_{MGJ}+S_{IDM}+S_{FME}\right)\)
Mà \(S_{MGJ}+S_{IDM}+S_{FME}=S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\)
\(\Rightarrow S_{ABC}\le3\left[S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\right]\)
\(\Rightarrow S_{AIMF}+S_{BGMD}+S_{CEMJ}\le\dfrac{2}{3}S_{ABC}\)