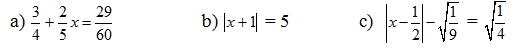ĐỀ 2I. PHẦN TRẮC NGHIỆM: (3 điểm) Khoanh tròn chữ cái đứng trước câu trả lời đúng: 1. Trong các khẳng định sau, khẳng định sai là:A. I ⊂ R B. I ∪ Q R C. Q ⊂ I D. Q ⊂ R2. Kết quả của phép nhân (-0,5)3.(-0,5) bằng:A. (-0,5)3 B. (-0,5) C. (-0,5)2 D. (0,5)43. Giá trị của (-2/3) ³ bằng:4. Nếu | x | |-9 |thì:A. x 9 hoặc x -9 B. x 9B. x -9 D. Không có giá trị nào của x để thỏa mãn5. Kết quả của phép tính 36.34. 32 bằng:A. 2712 B. 312...
Đọc tiếp
ĐỀ 2
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng:
1. Trong các khẳng định sau, khẳng định sai là:
A. I ⊂ R B. I ∪ Q = R C. Q ⊂ I D. Q ⊂ R
2. Kết quả của phép nhân (-0,5)3.(-0,5) bằng:
A. (-0,5)3 B. (-0,5) C. (-0,5)2 D. (0,5)4
3. Giá trị của (-2/3) ³ bằng:

4. Nếu | x | = |-9 |thì:
A. x = 9 hoặc x = -9 B. x = 9
B. x = -9 D. Không có giá trị nào của x để thỏa mãn
5. Kết quả của phép tính 36.34. 32 bằng:
A. 2712 B. 312 C. 348 D. 2748
6. Kết quả của phép tính 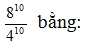
A. 2
0 B. 4
0 C. 2
20 D. 2
10II. PHẦN TỰ LUẬN: (7 điểm)
Bài 1: (1,5đ) Thực hiện phép tính (bằng cách hợp lí nhất nếu có thể).

Bài 2: (1,5đ) Tìm x, biết:
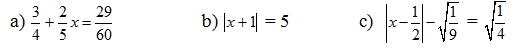
Bài 3: (2đ) Ba cạnh của tam giác lần lượt tỉ lệ với các số 3; 4; 5 và chu vi tam giác đó là 36 cm. Tính độ dài các cạnh của tam giác.
Bài 4: (2đ) Cho biểu thức A = 3/(x-1)
a) Tìm số nguyên x để A đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó.
b) Tìm số nguyên x để A đạt giá trị lớn nhất và tìm giá trị lớn nhất đó.