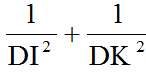Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Cho điểm A nằm ngoài đường thẳng xy và cách đường thẳng xy 3cm. Gọi M là điểm di động trê xy. Vẽ tam giác ABC vuông tại A sao cho AM là đường cao của tam giác đó. Tính giá trị nhỏ nhất của tích MB.MC?
Cho A nằm ngoài đường thẳng xy và cách đường thẳng xy là 3cm. Gọi M là điểm di động trên xy. Vẽ tam giác ABC vuông tại A sao cho AM là đường cao của tam giác đó. Tính GTNN của tích MB.MC
cho diem a nam ngoai duong thang xy va cach xy 3 cm. m la diem di dong tren xy ve tam giac abc vuong tai a sao cho am la duong cao cua tam giac do. tính GTNN cua MB.MC
Cho tam giác ABC vuông tại A (AB AC), đường cao AH. Gọi M là trung điểm BC. Biết AM 10cm và AH 8cm. a) Tính MH; AB; AC. b) Vẽ đường thẳng qua B và vuông góc với AM, cắt AC tại K. Tính BK, AK.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi M là trung điểm BC. Biết AM = 10cm và AH = 8cm. a) Tính MH; AB; AC. b) Vẽ đường thẳng qua B và vuông góc với AM, cắt AC tại K. Tính BK, AK.
Cho tam giác ABC (AB<AC) có góc A bằng 90* và M là trung tuyến của B. Gọi H là hình chiếu của A trên BC. Cho biết AM=13cm; AH=12cm
a) tính MH; AB; AC
b) Đường thẳng qua B và vuông góc với AM cắt AC tại F. Tính AF;BF
Bài 4. Cho đường tròn tâm O, đường kính AB = 10 cm và điểm C thuộc đường tròn sao cho AC=6 cm. Về CH vuông góc với AB tại H.
a) Chứng minh rằng tam giác ABC vuông tại C.
b) Tính HB và HC.
c) Trên tia đối của tia CA lấy điểm D sao cho CD= 2 cm. Gọi M là giao điểm của BD với đường tròn(M khác B). Chứng minh rằng CMD = CAB.
Cho tam giác ABC vuông tại A có đường cao là ah HP = 9 cm HC = 16 cm
a)tính AB AC ah
b)Gọi D và E lần lượt là hình chiếu vuông góc của h trên AB và AC. tứ giác AD he là hình gì
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.a) ΔANM là tam giác gì?b) Cmr: khi điểm M di động trên cạnh BC thì dfrac{1}{AM^2}+dfrac{1}{AE^2}không đổi A B C D N M
Đọc tiếp
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.
a) ΔANM là tam giác gì?
b) Cmr: khi điểm M di động trên cạnh BC thì \(\dfrac{1}{AM^2}+\dfrac{1}{AE^2}\)không đổi