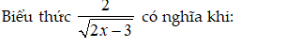Question

biểu thức sau đây xác định với giá trị nào của x

a√x^2-4 +2√x-2

b)3 √ x-3+√ x^2 -9

c)√ x+√ x+1

d)√ x+4 +√ x-1

 

Answer 1

`a)` Bth xác định `<=>{(x^2-4 >= 0),(x-2 >= 0):}<=>{(|x| >= 2),(x >= 2):}`

                                     `<=>{([(x >= 2),(x <= -2):}),(x >= 2):}<=>x >= 2`

__________________________________________________

`b)` Bth xác định `<=>{(x-3 >= 0),(x^2-9 >= 0):}<=>{(x >= 3),(|x| >= 3):}`

                                    `<=>{(x >= 3),([(x >= 3),(x <= -3):}):}<=>x >= 3`

__________________________________________________

`c)` Bth xác định `<=>{(x+1 >= 0),(x >= 0):}<=>{(x >= -1),(x >= 0):}<=>x >= 0`

__________________________________________________

`d` Bth xác định `<=>{(x+4 >= 0),(x-1 >= 0):}<=>{(x >= -4),(x >= 1):}<=>x >= 1`

Answer 2

biểu thức xác định khi ⇒\(\left\{{}\begin{matrix}x^2-4\ge0\\x-2\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left|x\right|\Rightarrow\ge2\\x\ge2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x\le-2\Leftrightarrow x\ge2\\x\ge2\end{matrix}\right.\\\\x\ge2\end{matrix}\right.\)