a.
\(p^2+p+2=p\left(p+1\right)+2\)
Do \(p\left(p+1\right)\) là tích 2 số tự nhiên liên tiếp nên luôn chẵn
\(\Rightarrow p\left(p+1\right)+2\) là số chẵn lớn hơn 2 nên là hợp số
b.
Với \(p=3\Rightarrow p^2+200=209\) chia hết 11 là hợp số
Với \(p\ne3\Rightarrow p^2\) chia 3 dư 1, mà 200 chia 3 dư 2
\(\Rightarrow p^2+200\) chia hết cho 3 với \(p\ne3\Rightarrow\) là hợp số
Vậy \(p^2+200\) là hợp số
Lời giải:
a.
Ta thấy: $p^2+p=p(p+1)$ là tích 2 số tự nhiên liên tiếp nên $p(p+1)\vdots 2$
$\Rightarrow p^2+p+2=p(p+1)+2\vdots 2$
Mà $p^2+p+2>2$ nên $p^2+p+2$ là hợp số
b.
Nếu $p$ chia hết cho $3$ thì $p=3$. Khi đó $p^2+200=209$ là hợp số
Nếu $p$ không chia hết cho $3$. Khi đó $p^2\equiv 1\pmod 3$
$\Rightarrow p^2+200\equiv 201\equiv 0\pmod 3$
Mà $p^2+200>3$ nên $p^2+200$ là hợp số
Vậy tóm lại $p^2+200$ là hợp số.
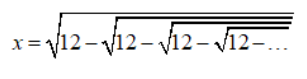thì x bằng bn
