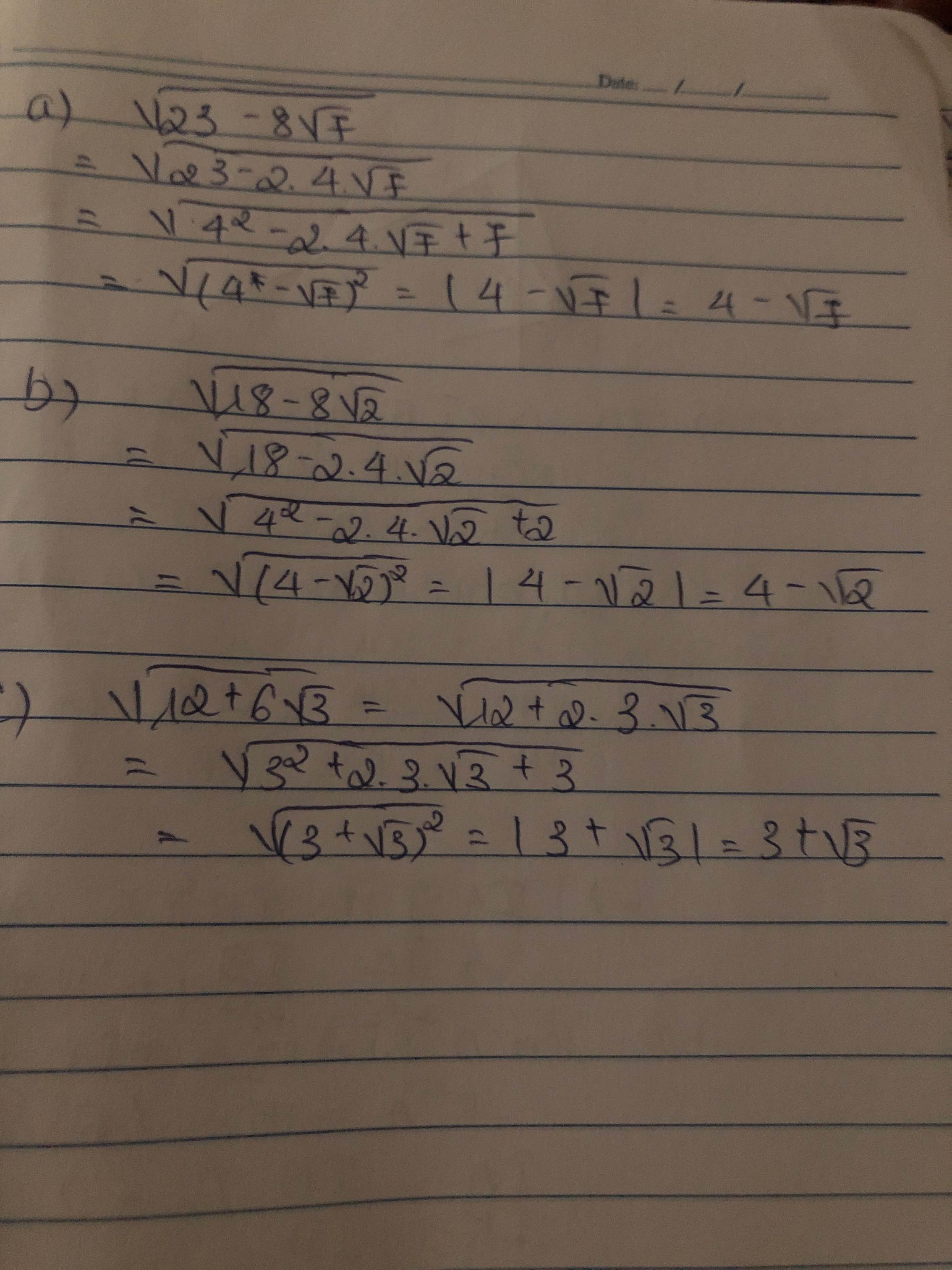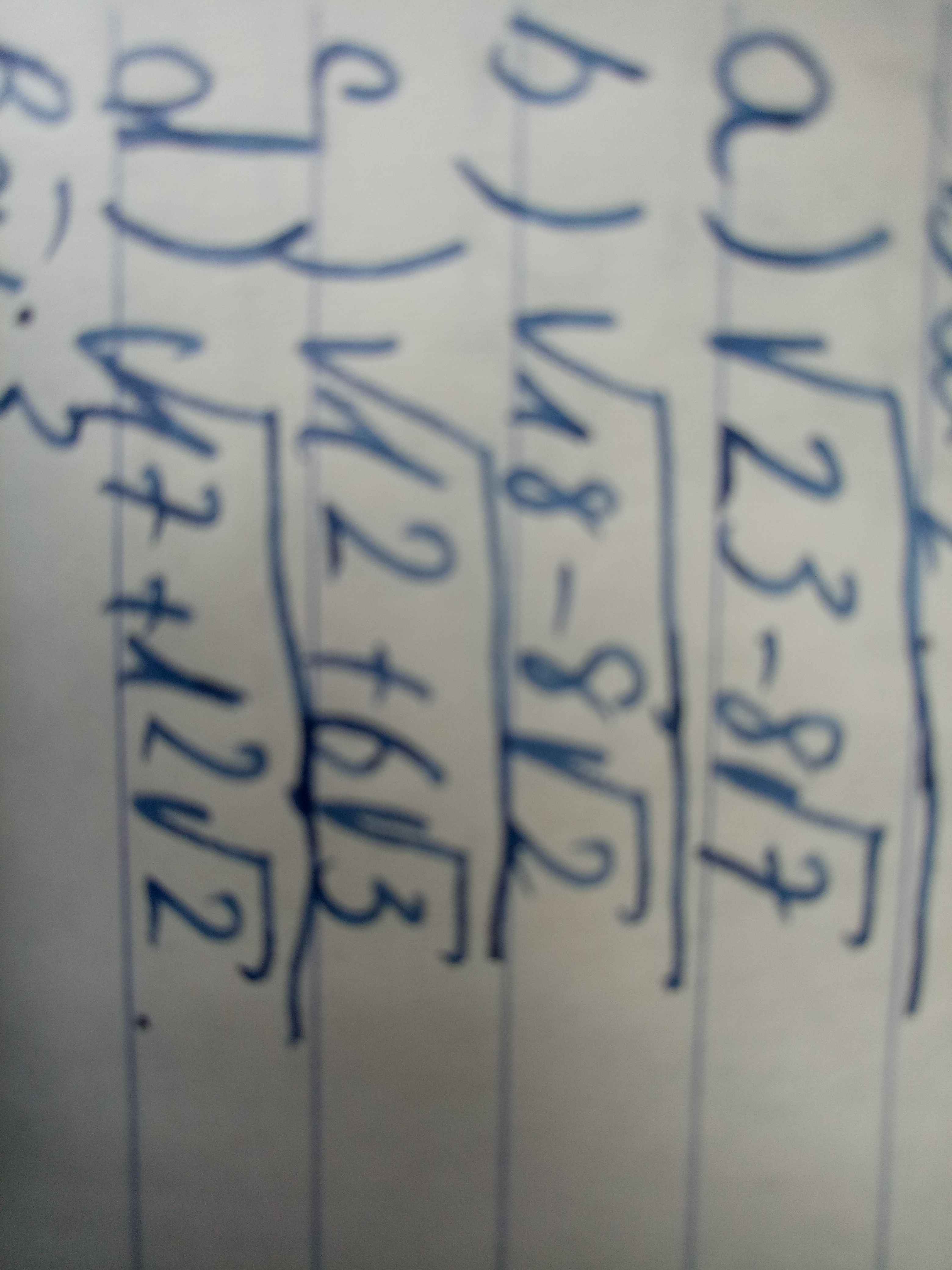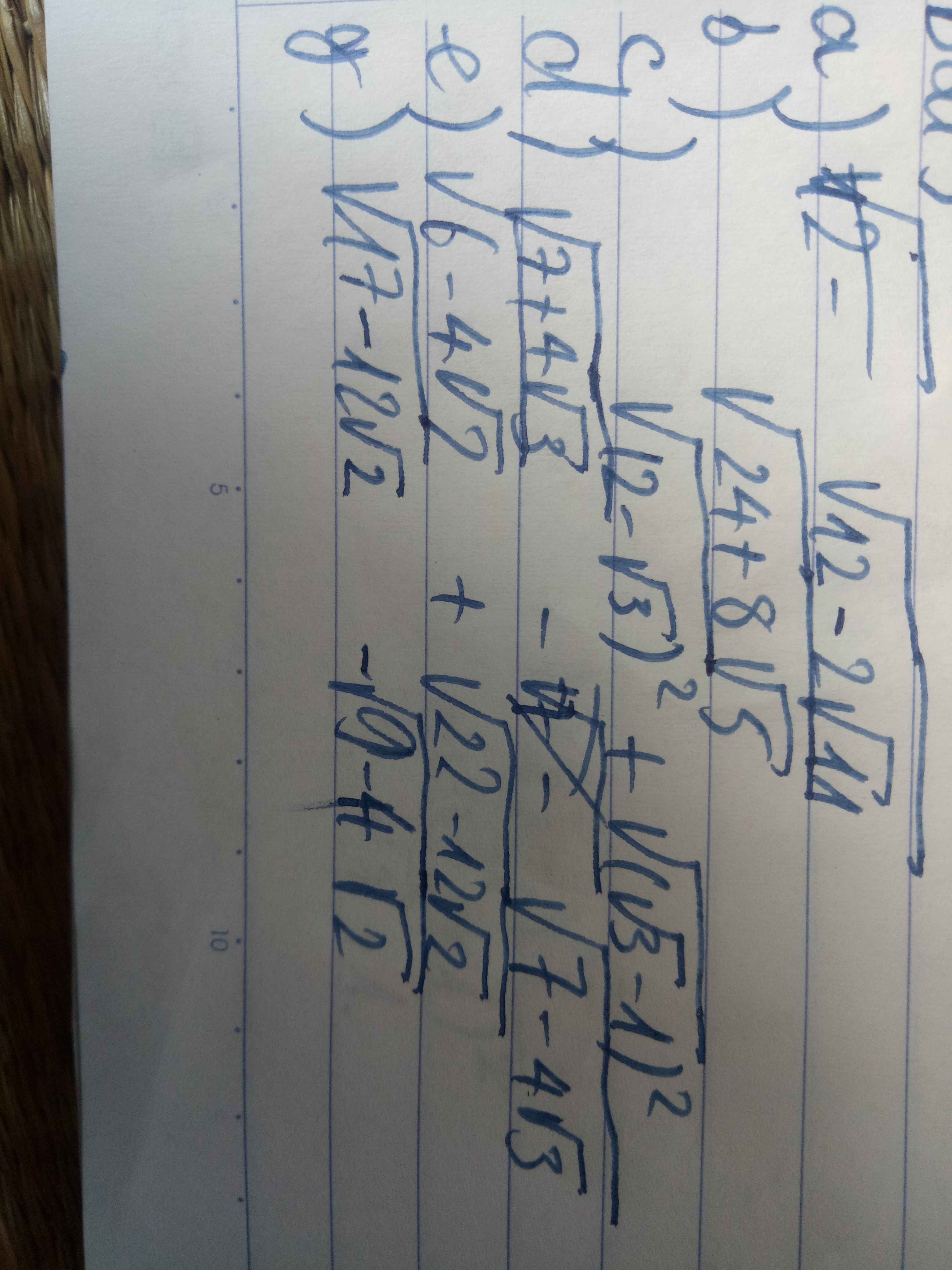Question

Bài 2 Rút gọn

Answer 1

Answer 2

d) \(\sqrt{17+12\sqrt{2}}=\sqrt{8+12\sqrt{2}+9}=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)

Answer 3

a) \(=\sqrt{16-8\sqrt{7}+7}\) \(=\sqrt{\left(4-\sqrt{7}\right)^2}\) \(=\left|4-\sqrt{7}\right|\) \(=4-\sqrt{7}\)

b) \(=\sqrt{16-8\sqrt{2}+2}\) \(=\sqrt{\left(4-\sqrt{2}\right)^2}\) \(=\left|4-\sqrt{2}\right|\) \(=4-\sqrt{2}\)

c) \(=\sqrt{9+6\sqrt{3}+3}\) \(=\sqrt{\left(3+\sqrt{3}\right)^2}\) \(=\left|3+\sqrt{3}\right|\) \(=3+\sqrt{3}\)

d) \(=\sqrt{17+6\sqrt{8}}\) \(=\sqrt{9+6\sqrt{8}+8}\) \(=\sqrt{\left(3+\sqrt{8}\right)^2}\) \(=\left|3+\sqrt{8}\right|\) \(=3+\sqrt{8}\) \(=3+2\sqrt{2}\)

Answer 4

\(a,\sqrt{23-8\sqrt{7}}\\ =\sqrt{16-8\sqrt{7}+7}\\ =\sqrt{\left(4-\sqrt{7}\right)^2}\\ =\left|4-\sqrt{7}\right|\\ =4-\sqrt{7}\)

\(b,\sqrt{18-8\sqrt{2}}\\ =\sqrt{16-8\sqrt{2}+2}\\ =\sqrt{\left(4-\sqrt{2}\right)^2}\\ =4-\sqrt{2}\)

\(c,\sqrt{12+6\sqrt{3}}\\ =\sqrt{9+6\sqrt{3}+3}\\ =\sqrt{\left(3+\sqrt{3}\right)^2}\\ =3+\sqrt{3}\)

\(d,\sqrt{17+12\sqrt{2}}\\ =\sqrt{9+12\sqrt{2}+8}\\ =\sqrt{\left(3+\sqrt{8}\right)^2}\\ =3+\sqrt{8}\)

Answer 5

a) \(\sqrt{23-8\sqrt{7}}=4-\sqrt{7}\)

b) \(\sqrt{18-8\sqrt{2}}=4-\sqrt{2}\)

c) \(\sqrt{12+6\sqrt{3}}=3+\sqrt{3}\)

d) \(\sqrt{17+12\sqrt{2}}=3+2\sqrt{2}\)