e: \(=x^3-3x^2y+3xy^2-y^3\)
f: \(=\dfrac{1}{2}x^2y^2\left(4x^2-y^2\right)=2x^4y^2-\dfrac{1}{2}x^2y^4\)
\(e,\left(x^2-2xy+y^2\right).\left(x-y\right)\)
\(=x^3-2x^2y+xy^2-x^2y-2xy^2+y^3\)
\(=x^3-3x^2y-xy^2+y^3\)
\(f,\dfrac{1}{2}x^2y^2.\left(2x+y\right).\left(2x-y\right)\)
\(=\left(x^3y^2+\dfrac{1}{2}x^2y^3\right).\left(2x-y\right)\)
\(=2x^4y^2-\dfrac{1}{2}x^2y^4\)













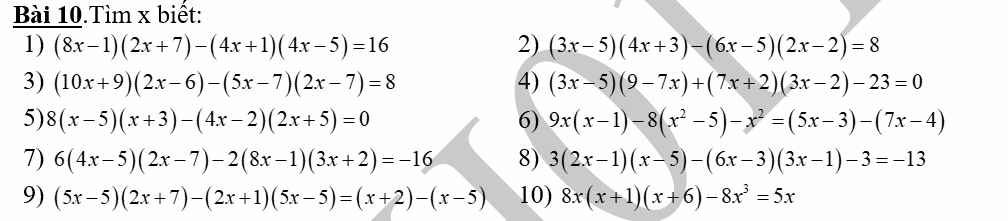 giúp em câu 6,9,10 câu này khó em k làm dc
giúp em câu 6,9,10 câu này khó em k làm dc![[Waanjai] Rùa](https://hoc24.vn/images/avt/avt29452625_256by256.jpg)
