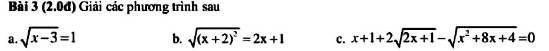Lời giải:
a. ĐKXĐ: $x\geq 3$
$\sqrt{x-3}=1$
$\Leftrightarrow x-3=1$
$\Leftrightarrow x=4$ (tm)
b. ĐKXĐ: $x\in\mathbb{R}$
$\sqrt{(x+2)^2}=2x+1$
$\Leftrightarrow (x+2)^2=(2x+1)^2$
$\Leftrightarrow (x+2)^2-(2x+1)^2=0$
$\Leftrightarrow (x+2-2x-1)(x+2+2x+1)=0$
$\Leftrightarrow (-x+1)(3x+3)=0$
$\Leftrightarrow x=1$ hoặc $x=-1$
c.
ĐKXĐ: $x\geq \frac{-1}{2}$
PT $\Leftrightarrow x+1+2\sqrt{2x+1}=\sqrt{x^2+8x+4}$
$\Rightarrow (x+1+2\sqrt{2x+1})^2=x^2+8x+4$
$\Leftrightarrow 2x+1+4(x+1)\sqrt{2x+1}=0$
$\Leftrightarrow \sqrt{2x+1}[\sqrt{2x+1}+4(x+1)]=0$
Hiển nhiên biểu thức trong ngoặc vuông >0 với mọi $x\geq \frac{-1}{2}$
Do đó $\sqrt{2x+1}=0$
$\Leftrightarrow x=\frac{-1}{2}$
Thử lại thấy thỏa mãn