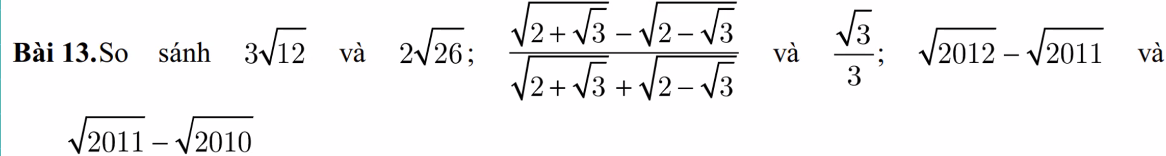Question

Answer 1

a: \(3\sqrt{12}=\sqrt{108}>\sqrt{104}=2\sqrt{26}\)

b: \(A=\dfrac{\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}}{\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}}\)

\(=\dfrac{\sqrt{3}+1-\sqrt{3}+1}{\sqrt{3}+1+\sqrt{3}-1}=\dfrac{2}{2\sqrt{3}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}=B\)

c: \(\sqrt{2012}-\sqrt{2011}=\dfrac{1}{\sqrt{2012}+\sqrt{2011}}\)

\(\sqrt{2011}-\sqrt{2010}=\dfrac{1}{\sqrt{2011}+\sqrt{2010}}\)

mà \(\sqrt{2012}>\sqrt{2010}\)

nên A<B