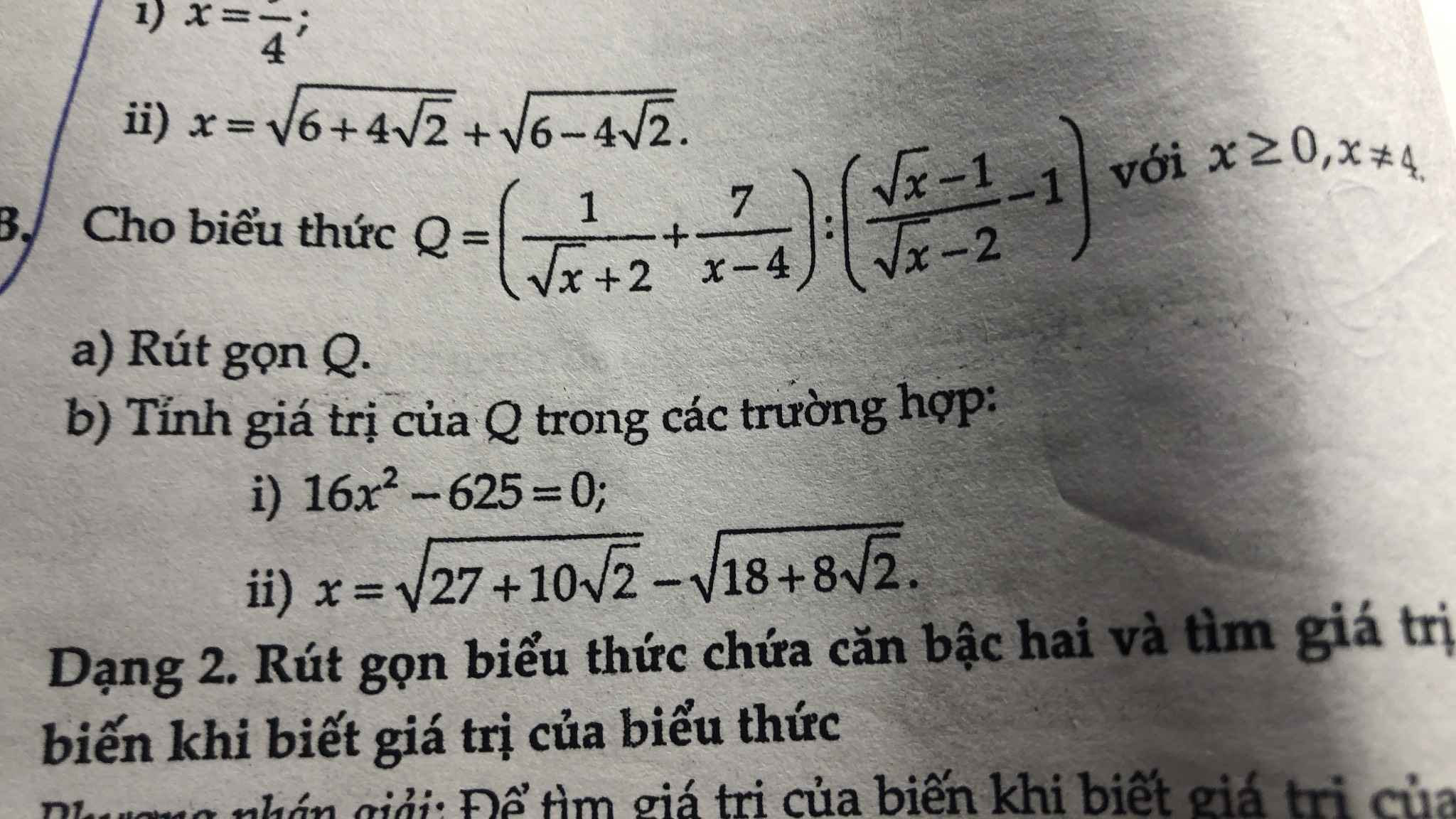a.
Ta có pttđ của Q:
\(Q=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{7}{x-4}\right):\left(\dfrac{\left(\sqrt{x}-1\right) \left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right)\)
\(Q=\left(\dfrac{\sqrt{x}-2}{x-4}+\dfrac{7}{x-4}\right):\left(\dfrac{x+\sqrt{x}-2}{x-4}-\dfrac{x-4}{x-4}\right)\)
\(Q=\dfrac{\sqrt{x}-2+7}{x-4}:\dfrac{x+\sqrt{x}-2-x+4}{x-4}\)
\(Q=\dfrac{\sqrt{x}+5}{x-4}:\dfrac{\sqrt{x}+2}{x-4}\)
\(Q=\dfrac{\sqrt{x}+5}{x-4}\times\dfrac{x-4}{\sqrt{x}+2}=\dfrac{\left(\sqrt{x}+5\right)\left(x-4\right)}{\left(x-4\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+5}{\sqrt{x}+2}\)
b.
ta tìm giá trị của x để thay vào tính giá trị của Q :
ta có:
i). biểu thức tương đương:
\(16x^2=625\)
=> \(x^2=\dfrac{625}{16}\)
=> \(x=\sqrt{\dfrac{625}{16}}=\dfrac{25}{4}\)
Với trường hợp i) có x có giá trị là \(\dfrac{25}{4}\) , thay x vào Q ta tính được giá trị của Q là:
\(Q=\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{\sqrt{\dfrac{25}{4}}+5}{\sqrt{\dfrac{25}{4}+2}}=\dfrac{5}{3}\)
ii ) . Biểu thức tương đương:
\(x=\sqrt{25+10\sqrt{2}+2}-\sqrt{16+8\sqrt{2}+2}\)
\(x=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}\)
\(x=5+\sqrt{2}-\left(4+\sqrt{2}\right)=5+\sqrt{2}-4-\sqrt{2}=1\)
Thay x có giá trị là 1 vào biểu thức Q ta được:
\(Q=\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{\sqrt{1}+5}{\sqrt{1}+2}=\dfrac{1+5}{1+2}=\dfrac{6}{3}=2\)
#N