`ĐKXĐ: x ne +- 2`
\(\dfrac{x-2}{x+2}+\dfrac{4x}{x^2-4}=\dfrac{x+2}{x-2}\\ \Leftrightarrow\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}+\dfrac{4x}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x+2\right)^2}{\left(x+2\right)\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x^2-4x+4}{\left(x+2\right)\left(x-2\right)}+\dfrac{4x}{\left(x+2\right)\left(x-2\right)}-\dfrac{x^2+4x+4}{\left(x+2\right)\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x^2-4x+4+4x-x^2-4x-4}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow\dfrac{-4x}{\left(x-2\right)\left(x+2\right)}=0\\ \Rightarrow-4x=0\\ \Leftrightarrow x=0\)
Vậy pt có tập nghiệm `S={0}`
\(\dfrac{x-2}{x+2}+\dfrac{4x}{x^2-4}=\dfrac{x+2}{x-2}\)
\(ĐK:x\ne\pm2\)
\(\Leftrightarrow\dfrac{\left(x-2\right)^2+4x}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\left(x-2\right)^2+4x=\left(x+2\right)^2\)
\(\Leftrightarrow x^2-4x+4+4x=x^2+4x+4\)
\(\Leftrightarrow4=4x+4\)
\(\Leftrightarrow4x=0\)
\(\Leftrightarrow x=0\left(tm\right)\)
Vậy \(S=\left\{0\right\}\)
\(\dfrac{x-2}{x+2}+\dfrac{4x}{x^2-4}=\dfrac{x+2}{x-2}\)
ĐKXĐ: \(x\ne2\)
\(\Leftrightarrow\dfrac{x-2}{x+2}+\dfrac{4x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
\(\Leftrightarrow\dfrac{\left(x-2\right)\left(x+2\right)+4x}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow x^2-4+4x=x^2-4\)
\(\Leftrightarrow x^2-4+4x-x^2+4=0\)
\(\Leftrightarrow4x=0\)
\(\Leftrightarrow x=0\)

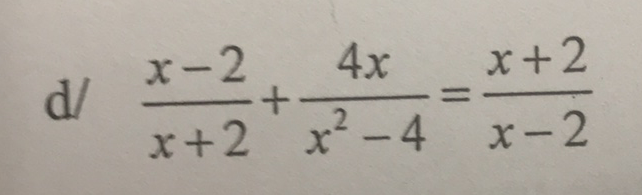

















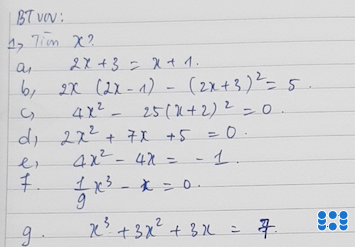

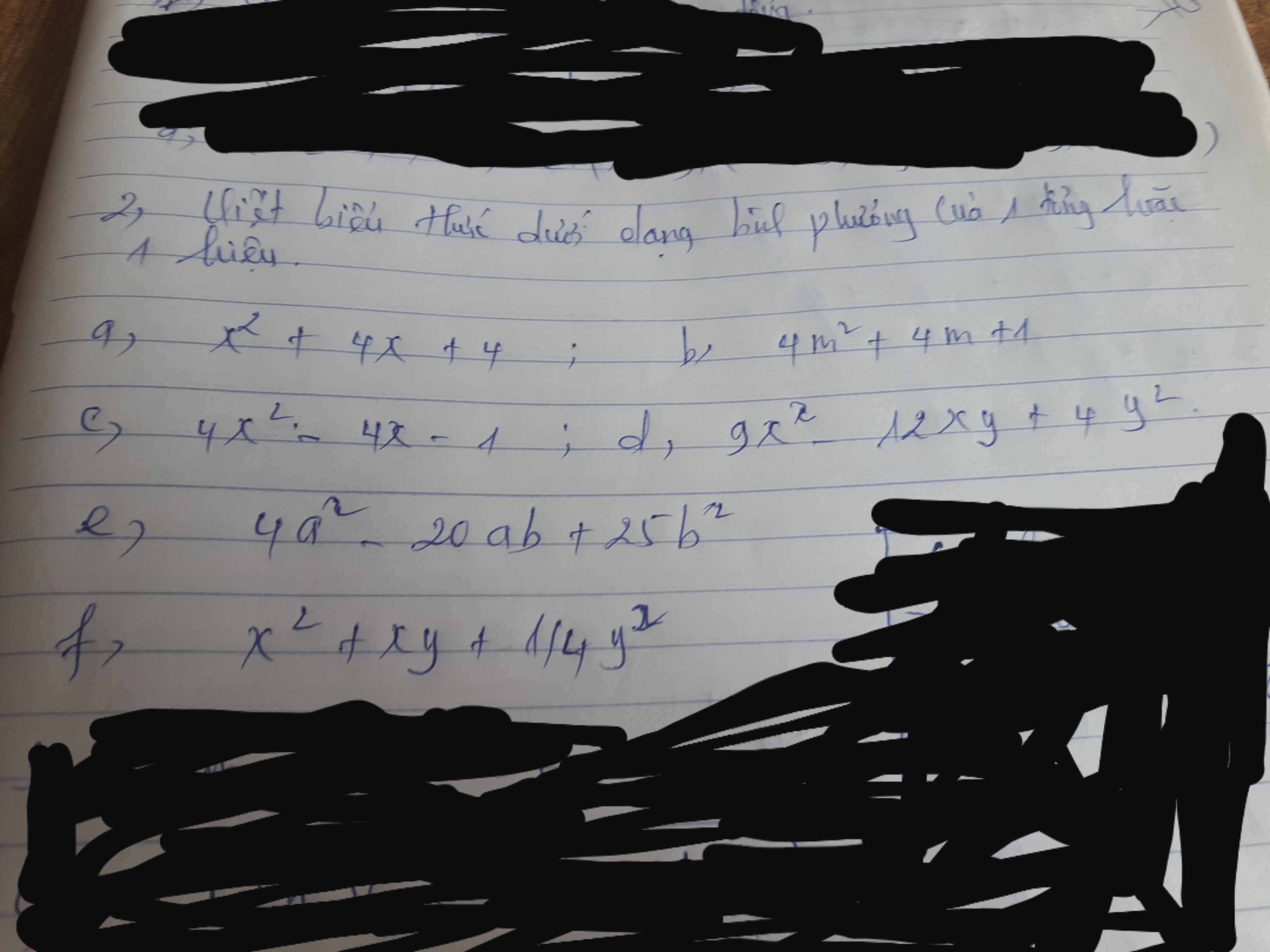


 giải thích giùm mình với
giải thích giùm mình với