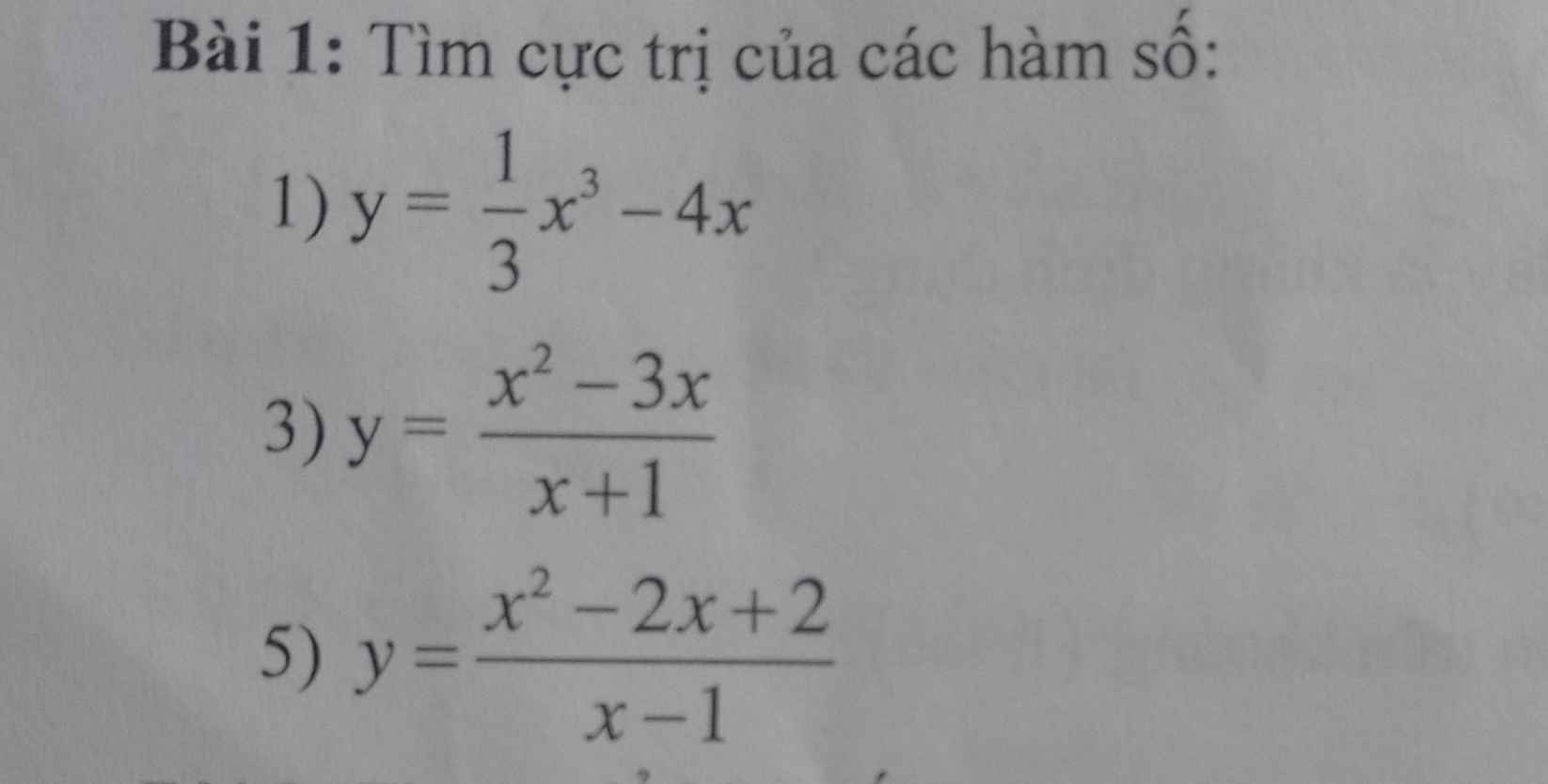1: y'=1/3*3x^2-4=x^2-4
y'=0
=>x=2 hoặc x=-2
=>y max=16/3 khi x=-2 và y min=-16/3 khi x=2
3: \(y'=\dfrac{\left(2x-3\right)\left(x+1\right)-\left(x^2-3x\right)}{\left(x+1\right)^2}=\dfrac{2x^2+2x-3x-3-x^2+3x}{\left(x+1\right)^2}\)
\(=\dfrac{x^2+2x-3}{\left(x+1\right)^2}\)
Đặt y'=0
=>x=-3 hoặc x=1
Lập bảng biến thiên, ta sẽ thấy là hàm số có cực đại là -9 khi x=-3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy , hình chiếu vuông góc của S trên đường thẳng AB là điểm H thuộc đoạn AB sao cho BH =2AH .Tính thể tích của khối chóp S.ABCD ?
Cho f'(x)=x2(x+1)(x2+2mx+5). có bao nhiêu giá trị m nguyên, m>-10 để hàm số g(x)=f(\(\left|x\right|\)) có 5 cực trị.
mọi người giúp e câu này vs ạ
cho x1, x2,...,x5 và \(\sum\limits^5_{i=1}\dfrac{1}{1+x_i}=1.\)Chứng minh rằng \(\sum\limits^5_{i=1}\dfrac{x_i}{a+x_i^2}\le1\)
tìm m để hàm số \(y=x^3+3x^2+\left(m+1\right)x+4m\) nghịch biến trên (-1;1)
tìm m để hàm số \(y=\dfrac{-x^3}{3}+\left(m-2\right)x^2-m\left(m-3\right)x-\dfrac{1}{3}\) nghịch biến trên \(\left(1;+\infty\right)\)
tìm m để hàm số \(y=x^3-\left(m+1\right)x^2-\left(2m^2-3m+2\right)x+2m^2-m\) đồng biến trên \(\left(2;+\infty\right)\)
Cho a, b là hai số nguyên dương sao cho cả hai hàm số y=ax+b4x+ay=ax+b4x+avà y=bx+a4x+by=bx+a4x+b đồng biến trên từng khoảng xác định. Giá trị nhỏ nhất của biểu thức S=a+b ?
khai triển maclaurin 1/((sinx)^2)) đến số hạng x^5
tìm m để hàm số \(=-x^4+\left(2m-3\right)x^2+m\) nghịch biến trên (1;3)
