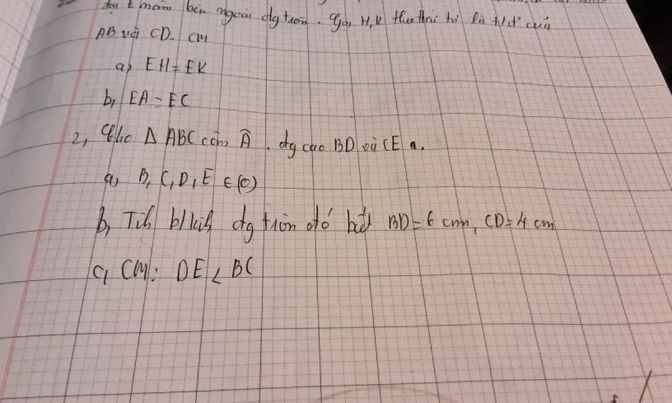Question

Answer 1

Bài 2: 

a: Xét tứ giác BCDE có 

\(\widehat{BEC}=\widehat{BDC}=90^0\)

Do đó: BCDE là tứ giác nội tiếp

hay B,C,D,E cùng thuộc (O)

Answer 2

a, Vì \(\widehat{BDC}=\widehat{BEC}=90^0\) nên BEDC nt đg tròn (O) đg kính BC

Do đó B,C,D,E∈O

b, Áp dụng PTG \(BC=\sqrt{BD^2+CD^2}=2\sqrt{13}\left(cm\right)\)

Mà BC là đg kính (O) nên bán kính có độ dài \(\dfrac{2\sqrt{13}}{2}=\sqrt{13}\left(cm\right)\)

c, Vì BC là đg kính (O) nên \(DE< BC\) do DE là dây cung