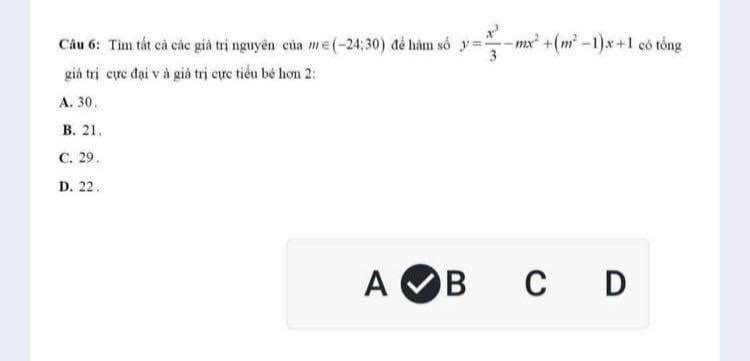
\(y'=x^2-2mx+m^2-1=\left(x-m\right)^2-1=\left(x-m+1\right)\left(x-m-1\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=m-1\\x=m+1\end{matrix}\right.\)
\(\Rightarrow y\left(m-1\right)+y\left(m+1\right)< 2\)
\(\Leftrightarrow\dfrac{\left(m-1\right)^3}{3}-m\left(m-1\right)^2+\left(m-1\right)\left(m^2-1\right)+1+\dfrac{\left(m+1\right)^3}{3}-m\left(m+1\right)^2+\left(m+1\right)\left(m^2-1\right)\le2\)
\(\Leftrightarrow\dfrac{2m}{3}\left(m^2-3\right)< 0\)
\(\Rightarrow\left[{}\begin{matrix}m< -\sqrt{3}\\0< m< \sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\) Có 23 giá trị (ko đáp án nào đúng?)
Đúng 0
Bình luận (0)
