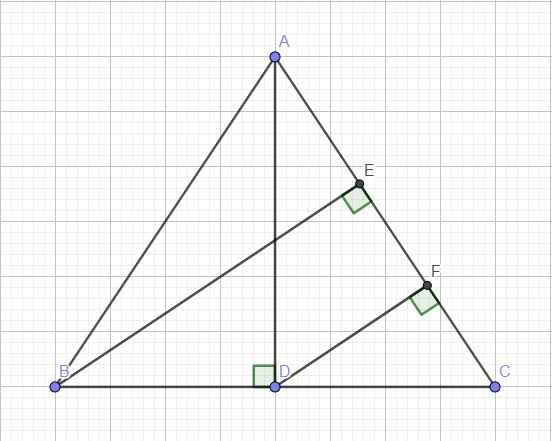
Giả sử tam giác ABC cân tại A với các đường cao \(AD=10\left(cm\right)\) và \(BE=12\left(cm\right)\)
Trong tam giác vuông ADC, kẻ đường cao DF (F thuộc AC)
Do DF và BE cùng vuông góc AC \(\Rightarrow DF||BE\) (1)
Lại có ABC cân tại A \(\Rightarrow D\) đồng thời là trung điểm BC (2)
(1); (2) \(\Rightarrow\) DF là đường trung bình tam giác BCE
\(\Rightarrow DF=\dfrac{1}{2}BE=6\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ADC:
\(\dfrac{1}{DF^2}=\dfrac{1}{AD^2}+\dfrac{1}{DC^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{DC^2}\Rightarrow DC=7,5\left(cm\right)\)
D là trung điểm BC \(\Rightarrow BC=2DC=15\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=75\left(cm^2\right)\)
Lời giải:
Giả sử tam giác $ABC$ cân tại $A$ có đường cao $AH=12, BK=10$ (cm)
$2S_{ABC}=AH.BC=BK.AC$
$\Rightarrow BC=\frac{BK}{AH}.AC=\frac{5}{6}AC$
$CH=\frac{BC}{2}=\frac{5}{12}AC$
Áp dụng định lý Pitago:
$AH^2=AC^2-CH^2$
$12^2=AC^2-(\frac{5}{12}AC)^2$
$144=\frac{144}{119}AC^2$
$AC=\frac{144}{\sqrt{119}}$ (cm)
$BC=\frac{5}{6}AC=\frac{120}{\sqrt{119}}$ (cm)
$S_{ABC}=\frac{AH.BC}{2}=\frac{12.120}{2\sqrt{119}}=\frac{720}{\sqrt{119}}$ (cm vuông)










 mong mn giúp em, em cần gấp
mong mn giúp em, em cần gấp





