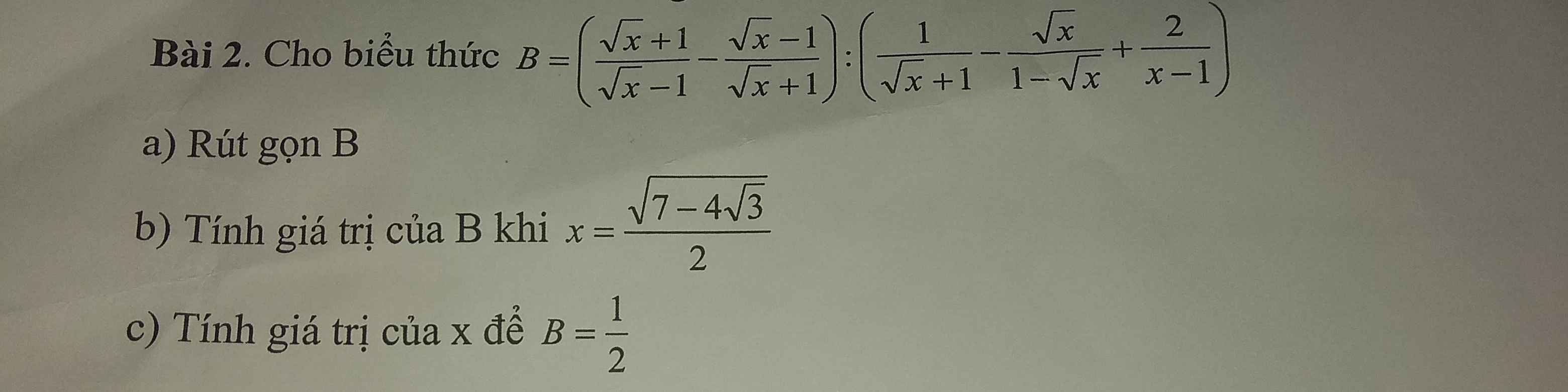Lời giải:
ĐKXĐ: $x\geq 0; x\neq 1$
a. \(B=\frac{(\sqrt{x}+1)^2-(\sqrt{x}-1)^2}{(\sqrt{x}-1)(\sqrt{x}+1)}:\left[\frac{\sqrt{x}-1+\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{2}{(\sqrt{x}-1)(\sqrt{x}+1)}\right]\)
\(=\frac{4\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}:\frac{x+2\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{4\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(\sqrt{x}+1)^2}=\frac{4\sqrt{x}}{(\sqrt{x}+1)^2}\)
b. \(x=\frac{\sqrt{7-4\sqrt{3}}}{2}=\frac{\sqrt{(2-\sqrt{3})^2}}{2}=\frac{|2-\sqrt{3}|}{2}=\frac{2-\sqrt{3}}{2}\)
\(x=\frac{4-2\sqrt{3}}{4}=\frac{(\sqrt{3}-1)^2}{2^2}\Rightarrow \sqrt{x}=\frac{\sqrt{3}-1}{2}\)
\(B=\frac{4.\frac{\sqrt{3}-1}{2}}{(\frac{\sqrt{3}-1}{2}+1)^2}=-20+12\sqrt{3}\)
c. \(B=\frac{1}{2}\Leftrightarrow \frac{4\sqrt{x}}{(\sqrt{x}+1)^2}=\frac{1}{2}\)
\(\Leftrightarrow 8\sqrt{x}=(\sqrt{x}+1)^2\)
\(\Leftrightarrow x-6\sqrt{x}+1=0\Leftrightarrow \sqrt{x}=3\pm 2\sqrt{2}\)
\(\Leftrightarrow x=17\pm 12\sqrt{2}\)