Hàm số nào sau đây là một nguyên hàm của hàm số y = x4?
A. \(-\dfrac{x^5}{5}.\) B. 4x3.
C. \(\dfrac{x^5}{5}+1\). D. - 4x3 - 1.
Hàm số nào sau đây là một nguyên hàm của hàm số y = x4?
A. \(-\dfrac{x^5}{5}.\) B. 4x3.
C. \(\dfrac{x^5}{5}+1\). D. - 4x3 - 1.
Hàm số nào sau đây là một nguyên hàm của hàm số \(y=\dfrac{1}{x^2}\)?
A. \(\dfrac{1}{x^3}\). B. \(-\dfrac{1}{x}\). C. \(\dfrac{1}{x}\). D. \(-\dfrac{1}{x^3}\).
Thảo luận (1)Hướng dẫn giảiTa có: \(\int {\frac{1}{{{x^2}}}dx} = \int {{x^{ - 2}}dx} = \frac{{{x^{ - 1}}}}{{ - 1}} + C = \frac{{ - 1}}{x} + C\)
Với \(C = 0\), ta sẽ thu được kết quả là hàm số ở đáp án B.
Vậy đáp án đúng là B.
(Trả lời bởi Nguyễn Quốc Đạt)
Khẳng định nào sau đây đúng?
A. \(\int\left(\cos x-2\sin x\right)dx=\sin x+2\cos x+C\)
B. \(\int\left(\cos x-2\sin x\right)dx=-\sin x+2\cos x+C\)
C. \(\int\left(\cos x-2\sin x\right)dx=\sin x-2\cos x+C\)
D. \(\int\left(\cos x-2\sin x\right)dx=-\sin x-2\cos x+C\)
Thảo luận (1)Hướng dẫn giảiTa có
\(\int {\left( {\cos x - 2\sin x} \right)dx} = \int {\cos xdx} - 2\int {\sin xdx} = \sin x - 2\left( { - \cos x} \right) + C = \sin x + 2\cos x + C\)
Vậy đáp án đúng là A.
(Trả lời bởi Nguyễn Quốc Đạt)
Khẳng định nào sau đây đúng?
A. \(\int\left(x-\dfrac{1}{x}\right)^2dx=\dfrac{x^3}{3}-2x-\dfrac{1}{x}+C.\)
B. \(\int\left(x-\dfrac{1}{x}\right)^2dx=\dfrac{x^3}{3}-2x+\dfrac{1}{x}+C.\)
C. \(\int\left(x-\dfrac{1}{x}\right)^2dx=\dfrac{1}{3}\left(x-\dfrac{1}{x}\right)^3+C.\)
D. \(\int\left(x-\dfrac{1}{x}\right)^2dx=\dfrac{1}{3}\left(x-\dfrac{1}{x}\right)^3\left(1+\dfrac{1}{x^2}\right)+C.\)
Thảo luận (1)Hướng dẫn giảiTa có
\(\int {{{\left( {x - \frac{1}{x}} \right)}^2}dx} = \int {\left( {{x^2} - 2 + \frac{1}{{{x^2}}}} \right)dx} = \int {{x^2}dx} - 2\int {dx} + \int {\frac{1}{{{x^2}}}dx} = \frac{{{x^3}}}{3} - 2x - \frac{1}{x} + C\)
Vậy đáp án đúng là A.
(Trả lời bởi Nguyễn Quốc Đạt)
Khẳng định nào sau đây đúng?
A. \(\int3^{2x}dx=\dfrac{9^x}{\ln}+C\). B. \(\int3^{2x}dx=9^x.\ln9+C\).
C. \(\int3^{2x}dx=\left(\dfrac{3^x}{\ln3}\right)^2+C\). D. \(\int3^{2x}dx=3^x.\ln3+C.\)
Thảo luận (1)Hướng dẫn giảiTa có \(\int {{3^{2x}}dx} = \int {{{\left( {{3^2}} \right)}^x}dx} = \int {{9^x}dx} = \frac{{{9^x}}}{{\ln 9}} + C\)
Vậy đáp án đúng là A.
(Trả lời bởi Nguyễn Quốc Đạt)
Giá trị của \(\int\limits^1_{-2}\left(4x^3+3x^2+8x\right)dx+\int\limits^2_1\left(4x^3+3x^2+8x\right)dx\) bằng
A. 16. B. −16. C. 52. D. 0.
Thảo luận (1)Hướng dẫn giảiTa có:
\(\int\limits_{ - 2}^1 {\left( {4{x^3} + 3{x^2} + 8x} \right)dx} + \int\limits_1^2 {\left( {4{x^3} + 3{x^2} + 8x} \right)dx} = \int\limits_{ - 2}^2 {\left( {4{x^3} + 3{x^2} + 8x} \right)dx} \)
\( = \left. {\left( {{x^4} + {x^3} + 4{x^2}} \right)} \right|_{ - 2}^2 = 40 - 24 = 16\)
Vậy đáp án đúng là A.
(Trả lời bởi Nguyễn Quốc Đạt)
Biết rằng \(\int\limits^2_0f\left(x\right)dx=-4\). Giá trị của \(\int\limits^2_0\left[3x-2f\left(x\right)\right]dx\) bằng
A. −2. B. 12. C. 14. D. 22.
Thảo luận (1)Hướng dẫn giảiTa có \(\int\limits_0^2 {\left[ {3x - 2f\left( x \right)} \right]dx} = \int\limits_0^2 {3xdx} - 2\int\limits_0^2 {f\left( x \right)dx} = \left. {\left( {\frac{{3{x^2}}}{2}} \right)} \right|_0^2 - 2.4 = \left( {6 - 0} \right) - 8 = - 2\)
Vậy đáp án đúng là A.
(Trả lời bởi Nguyễn Quốc Đạt)
Giá trị của \(\int\limits^2_0\left|x^2-x\right|dx\) bằng
A. \(\dfrac{2}{3}\). B. 1. C. \(\dfrac{1}{3}\). D. 2.
Thảo luận (1)Hướng dẫn giảiTa có \({x^2} - x = 0 \Leftrightarrow x = 0\) hoặc \(x = 1\).
Như vậy,
\(\int\limits_0^2 {\left| {{x^2} - x} \right|dx} = \int\limits_0^1 {\left| {{x^2} - x} \right|dx} + \int\limits_1^2 {\left| {{x^2} - x} \right|dx} = \left| {\int\limits_0^1 {\left( {{x^2} - x} \right)dx} } \right| + \left| {\int\limits_1^2 {\left( {{x^2} - x} \right)dx} } \right|\)
\( = \left| {\left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)} \right|_0^1} \right| + \left| {\left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)} \right|_1^2} \right| = \left| {\frac{{ - 1}}{6} - 0} \right| + \left| {\frac{2}{3} - \left( { - \frac{1}{6}} \right)} \right| = 1\)
Vậy đáp án đúng là B.
(Trả lời bởi Nguyễn Quốc Đạt)
Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số y = x3, y = x và hai đường thẳng x = 0, x = 2 bằng
A. \(\dfrac{2}{3}\). B. \(\dfrac{5}{2}\). C. \(\dfrac{9}{4}\). D. \(\dfrac{1}{4}\).
Thảo luận (1)Hướng dẫn giảiDiện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^3}\), \(y = x\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = \int\limits_0^2 {\left| {{x^3} - x} \right|dx} \).
Ta có \({x^3} - x = 0 \Leftrightarrow x = 0\) hoặc \(x = \pm 1\). Do đó:
\(S = \int\limits_0^1 {\left| {{x^3} - x} \right|dx} + \int\limits_1^2 {\left| {{x^3} - x} \right|dx} = \left| {\int\limits_0^1 {\left( {{x^3} - x} \right)dx} } \right| + \left| {\int\limits_1^2 {\left( {{x^3} - x} \right)dx} } \right| = \left| {\left. {\left( {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right)} \right|_0^1} \right| + \left| {\left. {\left( {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right)} \right|_1^2} \right|\)
\( = \left| { - \frac{1}{4}} \right| + \left| {\frac{9}{4}} \right| = \frac{5}{2}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tốc độ chuyển động v (m/s) của một ca nô trong khoảng thời gian 40 giây được thể hiện như Hình 1. Quãng đường đi được của ca nô trong khoảng thời gian này là
A. 400 m. B. 350 m. C. 310 m. D. 200 m.
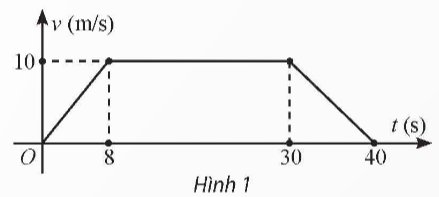
Thảo luận (1)Hướng dẫn giảiĐồ thị hàm số \(v\left( t \right)\) được chia thành 3 đường thằng \(OA\), \(AB\), \(BC\) như hình dưới đây.
Đường thẳng \(OA\) đi qua \(O\left( {0;0} \right)\) và \(A\left( {8;10} \right)\) nên phương trình đường thẳng \(OA\) là \(v = \frac{5}{4}t\).
Đường thẳng \(AB\) đi qua \(A\left( {8;10} \right)\) và \(B\left( {30;10} \right)\) nên phương trình đường thẳng \(AB\) là \(v = 10\).
Đường thẳng \(BC\) đi qua \(B\left( {30;10} \right)\) và \(C\left( {40;0} \right)\) nên phương trình đường thẳng \(BC\) là \(v = - t + 40\).
Vậy \(v\left( t \right) = \left\{ \begin{array}{l}\frac{5}{4}t{\rm{ }}\left( {0 \le t \le 8} \right)\\10{\rm{ }}\left( {8 \le t \le 30} \right)\\ - t + 40{\rm{ }}\left( {30 \le t \le 40} \right)\end{array} \right.\).
Do đó, quãng đường ca nô đi được trong 40 giây là
\(s = \int\limits_0^{40} {v\left( t \right)dt} = \int\limits_0^8 {v\left( t \right)dt} + \int\limits_8^{30} {v\left( t \right)dt} + \int\limits_{30}^{40} {v\left( t \right)dt} = \int\limits_0^8 {\frac{5}{4}tdt} + \int\limits_8^{30} {10dt} + \int\limits_{30}^{40} {\left( { - t + 40} \right)dt} \)
\( = \frac{5}{4}\left. {\left( {\frac{{{t^2}}}{2}} \right)} \right|_0^8 + 10\left. {\left( t \right)} \right|_8^{30} + \left. {\left( { - \frac{{{t^2}}}{2} + 40t} \right)} \right|_{30}^{40} = \frac{5}{4}.32 + 10.22 + 50 = 310\) (m).
Đáp án đúng là C
(Trả lời bởi Nguyễn Quốc Đạt)