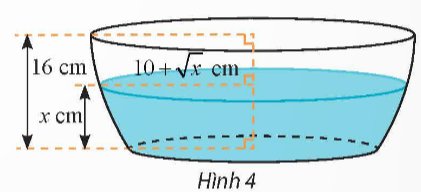
Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t) = 10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật.
a) Tính quãng đường s(t) vật di chuyển được sau thời gian t giây (trong khoảng thời gian vật đang rơi).
b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.