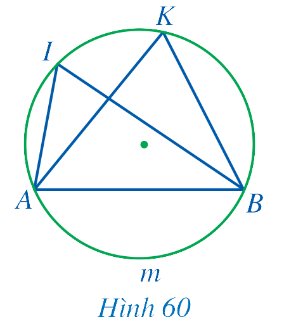
Quan sát Hình 60 và nêu mối liên hệ giữa:
a) \(\widehat{AIB}\) và sđ\(\stackrel\frown{AmB}\);
b) \(\widehat{AKB}\) và sđ\(\stackrel\frown{AmB}\);
c) \(\widehat{AIB}\) và \(\widehat{AKB}\).
Cho đường tròn \(\left(O\right)\) Acó 2 dây cung AB và CD sao cho tia AB và tia CD cắt nhau tại điểm E ở ngoài đường tròn. Đường thẳng kẻ từ E song song với AD cắt đường thẳng CB tại F. Khi đó ta có:
A. \(\widehat{EFC}=\frac{1}{2}\left(sđ\stackrel\frown{AC}+sđ\stackrel\frown{BD}\right)\)
B. \(\widehat{EFC}=\frac{1}{2}\left(sđ\stackrel\frown{CD}-sđ\stackrel\frown{AB}\right)\)
C. \(\widehat{EFC}=\frac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{CD}\right)\)
D. \(\widehat{EFC}=\frac{1}{2}\left(sđ\stackrel\frown{AB}-sđ\stackrel\frown{CD}\right)\)
Nếu vẽ luôn hình cho mình thì càng tốt nha !!!
Xin chân thành cảm ơn !!!
Cho ΔAOB có \(\widehat{AOB}=110^o\) . Vẽ đường tròn (O, OA). Gọi C là 1 điểm trên đường tròn (O) biết sđ \(\stackrel\frown{AC}=40^0\) . Tính số đo cung nhỏ \(\stackrel\frown{BC}\) và cung lớn \(\stackrel\frown{BC}\)
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính \(OC\perp AB\) . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\) . CMR
a) \(\stackrel\frown{AM}=\stackrel\frown{CN}\) và AM=CN
b) MN=CA=CB
GIẢI HỘ MK CÂU B) NHA![]()
b) Do \(\stackrel\frown{AM}=\stackrel\frown{CN}\) (theo câu a) => \(\widehat{AOM}=\widehat{CON}\)
Mà \(\widehat{AOM}+\widehat{MOC}=\widehat{AOC}=90^o\) => \(\widehat{NOC}+\widehat{MOC}=\widehat{MON}=90^o\)
Xét ΔOMN và ΔOAC có: \(\widehat{MON}=\widehat{AOC}=90^o\)
OA = OM (=bán kính nửa đường tròn)
OC = ON (=bán kính nửa đường tròn)
=> ΔOMN = ΔOAC (c.g.c) => MN = AC (2 cạnh tương ứng)
CMTT => ΔOMN = ΔOBC => MN = BC (2 cạnh tương ứng)
=> MN = AC = BC
cho nửa đường tròn ( O) đường kính AB . Vẽ bán kính OC\(\perp\)AB . Trên cung CA và CB lần lượt lấy các điểm M và N sao cho sđ\(\stackrel\frown{CM}=sđ\stackrel\frown{BN}\). CMR
a) \(\stackrel\frown{AM}=\stackrel\frown{CN}\) và AM=CN
b) MN=CA=CB
a) Xét (O) có
M là một điểm nằm trên cung \(\stackrel\frown{CA}\)(gt)
nên \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{MA}=sđ\stackrel\frown{CA}\)(1)
Xét (O) có
N là một điểm nằm trên cung \(\stackrel\frown{CB}\)(gt)
nên \(sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}=sđ\stackrel\frown{CB}\)(2)
Xét (O) có AB là đường kính(gt)
nên O là trung điểm của AB
Xét ΔCAB có
CO là đường cao ứng với cạnh AB(gt)
CO là đường trung tuyến ứng với cạnh AB(O là trung điểm của AB)
Do đó: ΔCAB cân tại C(Định lí tam giác cân)
⇒CA=CB
⇒\(sđ\stackrel\frown{CA}=sđ\stackrel\frown{CB}\)(3)
Từ (1), (2) và (3) suy ra \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}\)
mà \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\)(gt)
nên \(sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}\)
hay \(\stackrel\frown{AM}=\stackrel\frown{CN}\)(đpcm)
Xét (O) có
AM là dây cung(A,M∈(O))
CN là dây cung(C,N∈(O))
\(\stackrel\frown{AM}=\stackrel\frown{CN}\)(cmt)
Do đó: AM=CN(Liên hệ giữa cung và dây)
Cho đường tròn (O;R), lần lượt đặt theo một chiều kể từ A các cung \(\stackrel\frown{AB},\stackrel\frown{BC,}\stackrel\frown{CD}\) sao cho \(sđ\stackrel\frown{AB}=60^0,sđ\stackrel\frown{BC}=90^0,sđ\stackrel\frown{CD}=120^0\). CMR:
a) ABCD là hình thang cân
b) \(AC\perp BD\)
c) Gọi M, N lần lượt là trung điểm của CD, AB. Trên tia đối tia AD lấy P, gọi Q là giao điểm của PN và DB. CMR: MN là phân giác của góc \(\widehat{PMQ}\).
Cho hình vẽ, biết \(\widehat{F}\) = 50o , \(sđ\stackrel\frown{AB}\) = 40o . Chứng minh \(AD\perp BC\)
Trên một đường tròn lấy liên tiếp 3 cung AC,CD,DB sao cho sđ \(\stackrel\frown{AC}\)=sđ\(\stackrel\frown{CD}\)=sđ\(\stackrel\frown{DB}\)=60\(\)độ. Hai đường thẳng AC và BD cắt nhau ở E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau. Chứng minh rằng:
a. \(\widehat{AEB}\) =\(\widehat{BTC}\).
b. Chứng minh CD là tia phân giác của góc BCI
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính \(OC\perp AB\) . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho sđ\(\stackrel\frown{CM}=sđ\stackrel\frown{BN}\) . cmr :
a)cung AM = cung CN và AN=CN
b)MN=CA=CB
LÀM GIÚP MÌNH CÂU B) Ạ![]()
![]()
Cho đường tròn (O;R), vẽ dây AB sao cho sđ \(\stackrel\frown{AB}\) nhỏ = \(\dfrac{1}{2}\) sđ\(\stackrel\frown{AB}\) lớn. Tính diện tích \(\Delta\)AOB
Tham khảo ha:
https://hoidap247.com/cau-hoi/522596
\(Ta.có:\\ Sđ\stackrel\frown{AB}_{lớn}+Sđ\stackrel\frown{AB}_{nhỏ}=360^0\\ mà.Sđ\stackrel\frown{AB}_{lớn}=2Sđ\stackrel\frown{AB}_{nhỏ}\\ Sđ\stackrel\frown{AB}_{nhỏ}=Sđ\widehat{AOB}\\ nên.Sđ\stackrel\frown{AB}_{nhỏ}=120^0\\ Kẻ.OH\perp AB\Rightarrow\widehat{AOH}=60^0\\ \Rightarrow\Delta AOH.là.nửa.\Deltađều\\ \Rightarrow OH=\dfrac{OA}{2}=\dfrac{R}{2}.và.AH=\dfrac{R\sqrt{3}}{2}\)
\(Vì.OH\perp AB.nên.AB=2AH=2.\dfrac{R\sqrt{3}}{2}=R\sqrt{3}\\ Vậy.S_{OAB}=\dfrac{1}{2}AB.OH=\dfrac{R^2\sqrt{3}}{4}\)
Cho (O;R) và hai dây AB, AC, B thuộc \(\stackrel\frown{AC}\), AB = \(R\sqrt{2}\) , sđ \(\stackrel\frown{AC}=120^0\).
a, Tính sđ \(\stackrel\frown{AB}\) , sđ \(\stackrel\frown{BC}\)
b, Tính độ dài \(\stackrel\frown{AB}\), độ dài \(\stackrel\frown{BC}\), độ dài \(\stackrel\frown{AC}\) theo R.
c, Tính AC, BC theo R.
Help me!!!
a. Xét \(\Delta OAB:\)\(AB^2=2R^2\)
\(OA^2+OB^2=R^2+R^2=2R^2\)
Vậy \(\Delta OAB\) vuông tại O.
\(\Rightarrow l_{\stackrel\frown{AB}}=\frac{\pi R.90}{180}=\frac{1}{2}\pi R\)
Có: \(l_{\stackrel\frown{BC}}=l_{\stackrel\frown{AC}}-l_{\stackrel\frown{AB}}\)\(=\frac{\pi R.120}{180}-\frac{1}{2}\pi R\)\(=\frac{1}{6}\pi R\)
c.Ace Legona, Nguyễn Việt Lâm tính giùm mk.
\(\widehat{AOC}=120^0\Rightarrow\widehat{AOH}=60^0\)
\(\Rightarrow AH=OA.sin\widehat{AOH}=R.sin60^0=\frac{R\sqrt{3}}{2}\)
\(\Rightarrow AC=2AH=R\sqrt{3}\)
\(\widehat{BOC}=\widehat{AOC}-\widehat{AOB}=30^0\)
Kẻ \(CP\perp OB\Rightarrow\left\{{}\begin{matrix}CP=OC.sin\widehat{POC}=R.sin30^0=\frac{R}{2}\\OP=OC.cos\widehat{POC}=R.cos30^0=\frac{R\sqrt{3}}{2}\end{matrix}\right.\)
\(BP=OB-OP=R-\frac{R\sqrt{3}}{2}=\frac{R\left(2-\sqrt{3}\right)}{2}\)
Áp dụng Pitago cho tam giác BCP:
\(BC=\sqrt{BP^2+CP^2}=R\sqrt{2-\sqrt{3}}\)
Ace Legona, Rồng Đom Đóm, Nguyen, Nguyễn Thành Trương, Nguyễn Thị Ngọc Thơ, Nguyễn Thị Thảo Vy, Lê Anh Duy, Y, Nguyễn Huy Thắng, Khôi Bùi , Bonking, Ribi Nkok Ngok, Nguyễn Việt Lâm, svtkvtm, Akai Haruma, Mysterious Person, @Phùng Khánh Linh, ...