a, đk : x khác -2 ; 2 

\(\left(x+2\right)^2-8x=0\Leftrightarrow x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)(ktm) 

pt vô nghiệm 

b, đk : x khác -1 ; 1 

\(x\left(x+1\right)-5x+3=0\Leftrightarrow x^2-4x+3=0\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\Leftrightarrow x=1\left(ktm\right);x=3\left(tm\right)\)

a: =>x^2+4x-4x+1=0

=>x^2+1=0

=>Loại

b: =>2x-6+4=2x+2

=>-2=2(loại)

c: =>2(x+3)-2x-1=1

=>6-1=1

=>5=1(loại)

d =>x+3=0

=>x=-3(loại)

e: =>x^2-3x^2+3x-3x-2=0

=>-2x^2-2=0

=>x^2+1=0

=>Loại

a: \(=\dfrac{\left|x+2\right|}{x-1}\)

b: \(=x-2y-\left|x-2y\right|\)\(=\left[{}\begin{matrix}x-2y-x+2y=0\\x-2y+x-2y=2x-4y\end{matrix}\right.\)

c: \(=\dfrac{\left|x+2\right|}{\left(x+2\right)\left(x-2\right)}=\pm\dfrac{1}{x-2}\)

a) \(\Rightarrow\left(\dfrac{1}{2}x-\dfrac{1}{3}\right)^2=\dfrac{4}{25}\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-\dfrac{1}{3}=\dfrac{2}{5}\\\dfrac{1}{2}x-\dfrac{1}{3}=-\dfrac{2}{5}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{22}{15}\\x=-\dfrac{2}{15}\end{matrix}\right.\)

b) \(\Rightarrow\left(1-\dfrac{1}{4}x\right)^2=\dfrac{121}{49}\)

\(\Rightarrow\left[{}\begin{matrix}1-\dfrac{1}{4}x=\dfrac{11}{7}\\1-\dfrac{1}{4}x=-\dfrac{11}{7}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{16}{7}\\x=\dfrac{72}{7}\end{matrix}\right.\)

\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{x-4}\cdot\dfrac{x-4}{4}=\dfrac{2\sqrt{x}}{4}=\dfrac{1}{2}\sqrt{x}\)

Với x < 0 ; x ≠ 0 ta có:

\(B=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{4}{x-4}\)

\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{x-4}\cdot\dfrac{x-4}{4}\)

\(=\dfrac{2\sqrt{x}}{4}=\dfrac{\sqrt{x}}{2}\)

Vậy \(B=\dfrac{\sqrt{x}}{2}\).

Chia nhỏ ra

a: =>1/2x=7/2-2/3=21/6-4/6=17/6

=>x=17/3

b: =>2/3:x=-7-1/3=-22/3

=>x=2/3:(-22/3)=-1/11

c: =>1/3x+2/5x-2/5=0

=>11/15x=2/5

hay x=6/11

d: =>2x-3=0 hoặc 6-2x=0

=>x=3/2 hoặc x=3

Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)

\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)

\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)

\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)

\(f\left(t\right)=t^4-5t^2+t+4\)

Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)

\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)

\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm

\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)

\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)

\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)

\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)

Dấu \(f'\left(t\right)\):

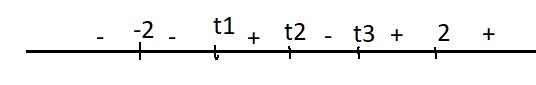
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)

Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)

\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)

\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)

1.

\(x^4-6x^2-12x-8=0\)

\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)

\(\Leftrightarrow x=1\pm\sqrt{5}\)

3.

ĐK: \(x\ge-9\)

\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)

\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)

\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)

Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)

\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)

\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)

\(\Leftrightarrow...\)

2.

ĐK: \(x\ne\dfrac{2\pm\sqrt{2}}{2};x\ne\dfrac{-2\pm\sqrt{2}}{2}\)

\(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{1}{2x+\dfrac{1}{x}+4}+\dfrac{1}{2x+\dfrac{1}{x}-4}=\dfrac{3}{5}\)

Đặt \(2x+\dfrac{1}{x}+4=a;2x+\dfrac{1}{x}-4=b\left(a,b\ne0\right)\)

\(pt\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{5}\left(1\right)\)

Lại có \(a-b=8\Rightarrow a=b+8\), khi đó:

\(\left(1\right)\Leftrightarrow\dfrac{1}{b+8}+\dfrac{1}{b}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{2b+8}{\left(b+8\right)b}=\dfrac{3}{5}\)

\(\Leftrightarrow10b+40=3\left(b+8\right)b\)

\(\Leftrightarrow\left[{}\begin{matrix}b=2\\b=-\dfrac{20}{3}\end{matrix}\right.\)

TH1: \(b=2\Leftrightarrow...\)

TH2: \(b=-\dfrac{20}{3}\Leftrightarrow...\)

a) \(\dfrac{y}{x}\cdot\sqrt{\dfrac{x^2}{y^4}}\)

\(=\dfrac{y}{x}\cdot\dfrac{\sqrt{x^2}}{\sqrt{\left(y^2\right)^2}}\) 

\(=\dfrac{y}{x}\cdot\dfrac{x}{y^2}\)

\(=\dfrac{1}{y}\)

b) \(\dfrac{5}{2}x^3y^3\cdot\sqrt{\dfrac{16}{x^4y^8}}\)

\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{\sqrt{16}}{\sqrt{\left(x^2y^4\right)^2}}\)

\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{4}{x^2y^4}\)

\(=\dfrac{20x^3y^3}{2x^2y^4}\)

\(=\dfrac{10x}{y}\)

c) \(ab^2\sqrt{\dfrac{3}{a^2b^4}}\)

\(=ab^2\dfrac{\sqrt{3}}{\sqrt{\left(ab^2\right)^2}}\)

\(=ab^2\cdot\dfrac{\sqrt{3}}{ab^2}\)

\(=\sqrt{3}\)

\(a,\dfrac{y}{x}\cdot\sqrt{\dfrac{x^2}{y^4}}\left(y\ge0;x,y\ne0\right)\) (sửa đề)

\(=\dfrac{y}{x}\cdot\dfrac{\sqrt{x^2}}{\sqrt{y^4}}\)

\(=\dfrac{y}{x}\cdot\dfrac{x}{\sqrt{\left(y^2\right)^2}}\)

\(=\dfrac{y}{x}\cdot\dfrac{x}{y^2}\)

\(=\dfrac{1}{y}\)

\(---\)

\(b,\dfrac{5}{2}x^3y^3\cdot\sqrt{\dfrac{16}{x^4y^8}}\left(x,y\ne0\right)\)

\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{\sqrt{16}}{\sqrt{x^4y^8}}\)

\(=\dfrac{5x^3y^3}{2}\cdot\dfrac{4}{x^2y^4}\)

\(=\dfrac{5x\cdot2}{y}\)

\(=\dfrac{10x}{y}\)

\(---\)

\(c,ab^2\sqrt{\dfrac{3}{a^2b^4}}\left(a>0;b\ne0\right)\) (sửa đề)

\(=ab^2\cdot\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}\)

\(=\dfrac{ab^2\sqrt{3}}{\sqrt{\left(ab^2\right)^2}}\)

\(=\dfrac{ab^2\sqrt{3}}{ab^2}\)

\(=\sqrt{3}\)

#\(Toru\)