Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)
\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)
\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)
\(f\left(t\right)=t^4-5t^2+t+4\)
Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)
\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm
\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)
\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)
\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)
\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)
Dấu \(f'\left(t\right)\):
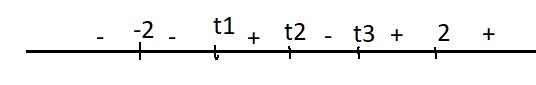
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)
Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)
\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)









