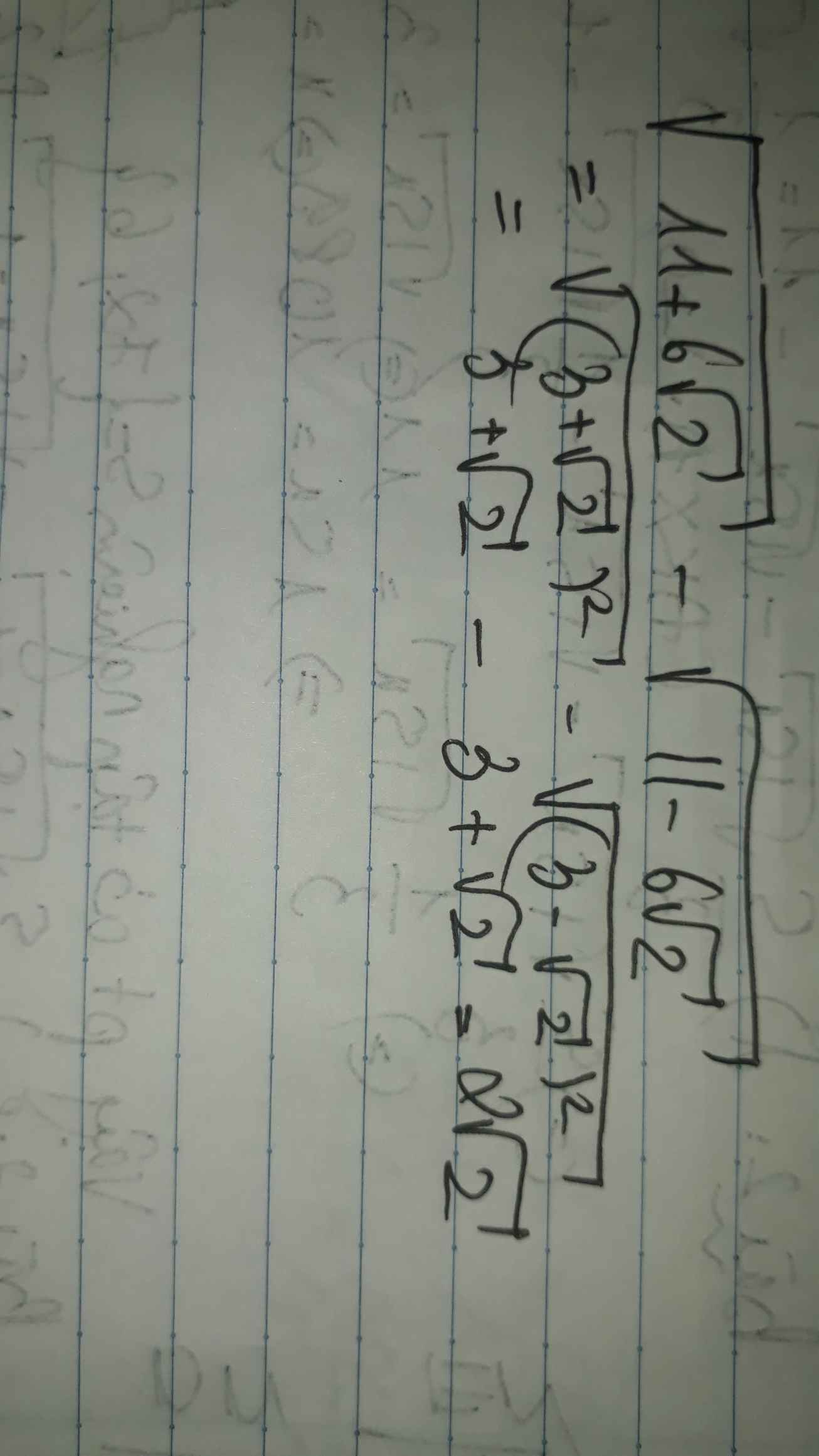`a, 2/7 +(3/7 + 5/7)= 2/7 + 3/7 + 5/7=(2/7 +5/7)+3/7= 1+3/7=7/7+3/7=10/7`

`b, (6/11+5/11)+4/11= 11/11+4/11=15/11`

`c, (5/6 + 7/6)+2/6= 12/6 + 2/6= 14/6= 7/3`

`@ yl`

\(a\) \(\dfrac{2}{7}+\left(\dfrac{3}{7}+\dfrac{5}{7}\right)=\dfrac{2}{7}+\dfrac{8}{7}=\dfrac{10}{7}\)

\(b\) \(\left(\dfrac{6}{11}+\dfrac{5}{11}\right)+\dfrac{4}{11}=\dfrac{11}{11}+\dfrac{4}{11}=\dfrac{15}{11}\)

\(c\) \(\left(\dfrac{5}{6}+\dfrac{7}{6}\right)+\dfrac{2}{6}=\dfrac{12}{6}+\dfrac{2}{6}=\dfrac{14}{6}=\dfrac{7}{3}\)

\(4.3^{x-1}+2.3^{x+2}=4.3^6+2.3^9\)

\(3^{x-1}.\left(4+2.3^3\right)=3^6.\left(4+2.3^3\right)\)

\(\Leftrightarrow3^{x-1}=3^6\)

\(\Leftrightarrow x-1=6\)

\(\Leftrightarrow x=7\)

Vậy \(x=7\)

\(5^{x+4}-3.5^{x+3}=2.5^{11}\)

\(\Leftrightarrow5^{x+3}.\left(5-3\right)=2.5^{11}\)

\(\Leftrightarrow5^{x+3}.2=2.5^{11}\)

\(\Leftrightarrow5^{x+3}=5^{11}\)

⇔\(x+3=11\)

\(\Leftrightarrow x=8\)

Vậy \(x=8\)

\(11.6^{x-1}=11.6^{11}+2.6^{13}\)

\(\Rightarrow11.6^{x-1}=6^{11}.\left(11+2.36\right)\)

\(\Rightarrow11.6^{x-1}=6^{11}.83\)

Ta có VT:

\(VT=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)

\(=\sqrt{3^2+2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}+\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)

\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)

\(=\left|3+\sqrt{2}\right|+\left|3-\sqrt{2}\right|\)

\(=3+\sqrt{2}+3-\sqrt{2}\)

\(=6=VP\left(dpcm\right)\)

\(VT=\sqrt{9+2\cdot3\cdot\sqrt{2}+2}+\sqrt{9-2\cdot3\cdot\sqrt{2}+2}\)

\(=3+\sqrt{2}+3-\sqrt{2}\)

=6=VP

a: \(=\dfrac{-3-5-7}{4}=\dfrac{-15}{4}\)

b: \(=\dfrac{-6-5-2+6}{11}=\dfrac{-7}{11}\)

a: \(\left(3+\sqrt{2}\right)^2=3^2+2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2\)

\(=9+6\sqrt{2}+2=11+6\sqrt{2}\)

b: \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)

\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)

\(=3+\sqrt{2}+3-\sqrt{2}=6\)

c: \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)

\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\)

\(=\sqrt{7}-1-\sqrt{7}-1=-2\)

d: \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)

\(=\sqrt{45-2\cdot3\sqrt{5}\cdot2+4}-\sqrt{45+2\cdot3\sqrt{5}\cdot2+4}\)

\(=\sqrt{\left(3\sqrt{5}-2\right)^2}-\sqrt{\left(3\sqrt{5}+2\right)^2}\)

\(=3\sqrt{5}-2-3\sqrt{5}-2=-4\)

a) \(\left(3+\sqrt{2}\right)^2=9+6\sqrt{2}+2=11+6\sqrt{2}\)

b) \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)

\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)

\(=3+\sqrt{2}+3-\sqrt{2}=6\)

c) \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)

\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\)

\(=\sqrt{7}-1-\sqrt{7}-1=-2\)

d) \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)

\(=\sqrt{\left(3\sqrt{5}-2\right)^2}-\sqrt{\left(3\sqrt{5}+2\right)^2}\)

\(=3\sqrt{5}-2-3\sqrt{5}-2=-4\)

\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)

\(=3+\sqrt{2}-3+\sqrt{2}\)

\(=2\sqrt{2}\)

L: \(\dfrac{7}{6}\) +\(\dfrac{8}{6}\) = \(\dfrac{15}{6}\)

T: \(\dfrac{1}{11}\) + \(\dfrac{7}{11}\) + \(\dfrac{9}{11}\) = \(\dfrac{17}{11}\)

Ạ: \(\dfrac{4}{11}\) + \(\dfrac{2}{11}\) = \(\dfrac{6}{11}\)

Đ: \(\dfrac{3}{6}\) + \(\dfrac{1}{6}\) + \(\dfrac{7}{6}\) = \(\dfrac{11}{6}\)

À: \(\dfrac{3}{11}\) + \(\dfrac{9}{11}\) = \(\dfrac{12}{11}\)

ĐÀ LẠT

Bn ghi đề vào nhé .

mik tick cho

3/11 x 2 = 6/11

6/11 : 3/11 = 2

6/11 : 2 = 3/11

2/3 x 11 = 22/3

4/2 x 7 = 14

8/7 : 2/7 = 4

8/7 : 4 = 2/7

2/7 x 4 = 8/7