Số nghiệm của phương trình l g ( x 2 - 6 x + 7 ) = l g ( x - 3 ) là
A. 2 B. 1
C. 0 D. Vô số
Cho hàm số g ( x ) = 2 x 2 + x 2 - 8 x Có bao nhiêu số nguyên m để phương trình g ( g ( x ) + 3 ) - m = 2 g ( x ) + 7 có đúng 6 nghiệm thực phân biệt
A. 7
B. 8
C. 24
D. 25
Phương trình \(\sqrt{2-f\left(x\right)}=f\left(x\right)\) có tập nghiệm A = {1;2;3}. Phương trình \(\sqrt{2.g\left(x\right)-1}+\sqrt[3]{3.g\left(x\right)-2}=2.g\left(x\right)\) có tập nghiệm là B = {0;3;4;5} . Hỏi tập nghiệm của phương trình \(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)+1=f\left(x\right)+g\left(x\right)\)
có bao nhiêu phần tử?
A.1
B.4 C.6 D.7
\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử
Cho 2 đa thức sau :
f(x) = ( x+1)( x-2 )
g(x) = x^3 +ax^2 + bx - 6
Biết rằng nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x). Chứng tỏ rằng g(x) cũng nhận x = -3 làm nghiệm
Đặt f(x)=0
=>x+1=0 hoặc x-2=0
=>x=-1 hoặc x=2
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}g\left(-1\right)=0\\g\left(2\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1+a-b-6=0\\8+4a+2b-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=7\\4a+2b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-5\end{matrix}\right.\)
Vậy: \(g\left(x\right)=x^3+2x^2-5x-6\)
g(-3)=-27+18+15-6=0
=>x=-3 là nghiệm của g(x)
tìm x;y trong phương trình nghiệm nguyên sau:
k)x^2+xy+y^2=7
g)x(x+1)=y^2-6
Phương trình 2 - f ( x ) = f ( x ) có tập nghiệm T 1 = 20 ; 18 ; 3 . Phương trình 2 g ( x ) - 1 + 3 g ( x ) - 2 3 = 2 g ( x ) có tập nghiệm T 2 = 0 ; 3 ; 15 ; 19 . Hỏi tập nghiệm của phương trình f ( x ) g ( x ) + 1 = f ( x ) + g ( x ) có bao nhiêu phần tử?
A. 4
B. 3
C. 11
D. 6
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
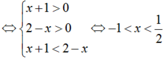
Gọi E là tập nghiệm của phương trình \({x^2} - 2x - 3 = 0\).
G là tập nghiệm của phương trình \((x + 1)(2x - 3) = 0\)
Tìm \(P = E \cap G\).
Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)
1/ Cho hai đa thức f(x) = 5x - 7 và g(x) = 3x + 1
a) Tìm nghiệm của hai đa thức trên
b) Tính h(x) = f(x) - g(x) và tìm nghiệm của h(x)
2/ Cho f(x) = x2 + 4x - 5
a) Số -5 có phải là nghiệm của f(x) không?
b) Tính g(x) biết g(x) - f(x) = 2x + 7
Bài 1:
a) Ta có:
\(f(x)=5x-7=0\Leftrightarrow 5x=7\Leftrightarrow x=\frac{7}{5}\)
\(g(x)=3x+1=0\Leftrightarrow 3x=-1\Leftrightarrow x=-\frac{1}{3}\)
Vậy $x=\frac{7}{5}$ và $x=-\frac{1}{3}$ lần lượt là nghiệm của đa thức $f(x)$ và $g(x)$
b)
\(h(x)=f(x)-g(x)=5x-7-(3x+1)=2x-8\)
\(h(x)=0\Leftrightarrow 2x-8=0\Leftrightarrow x=4\)
Vậy $x=4$ là nghiệm của đa thức $h(x)$
Bài 2:
a) Thay $x=-5$ vào đa thức $f(x)$:
\(f(-5)=(-5)^2+4(-5)-5=0\) nên $-5$ là nghiệm của $f(x)$
b)
\(g(x)-f(x)=2x+7\)
\(\Leftrightarrow g(x)=f(x)+2x+7=x^2+4x-5+2x+7\)
\(\Leftrightarrow g(x)=x^2+6x+2\)
Ta có : f(x) = x2 + x - 2 = ( x - 1 ) ( x + 2 )

Vậy a = 0 , b = \(-3\)
1) Phương trình 3x-5x+5= -8 có nghiệm là?
2) Giá trị của m để cho phương trình sau nhận x=2 làm nghiệm : 3x-2m=x+5 là?
3) Tập nghiệm của p.trình \(\frac{5x+4}{10}+\frac{2x+5}{6}=\frac{x-7}{15}-\frac{x+1}{30}\) là?
4) Nghiệm của p.trình \(\frac{5x-3}{6}-x+1=1-\frac{x+1}{3}\)
5) Nghiệm của p.trình -8( 1,3-2x)=4(5x+1) là?
6) Nghiệm của p.trình \(\frac{8x+5}{4}-\frac{3x+1}{2}=\frac{2x+1}{2}+\frac{x+4}{4}\)là?
7) Nghiệm của p.trình \(\frac{2\left(x+6\right)}{3}+\frac{x+13}{2}-\frac{5\left(x-1\right)}{6}=\frac{x+1}{3}+11\)
8) Phương trình m(x-1)=5-(m-1)x vô nghiệm nếu?
9) Phương trình (2x-3)(3x+2)=6x(x-50)+44 có nghiệm là?