thứ nhất bn đăng sai môn 

thứ hai bn giải r đăng lmj :???

Thứ nhất đang sai môn 

Thứ hai không biết giải fndf]-0jhdfuhiofghjfgoihjfgopihjfgihjohjgo;hjghghgdjhldhjdfighjs;dligjlkdfgjdhfghfgh41fg6j541fg3j5h4gf6j54dgh65gf4654j

5gj5fg

35j4gh

6jfd4

5j4fj

😱😱😱😱😱😱😱😱😱😱😱

1.

\(x^4-6x^2-12x-8=0\)

\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)

\(\Leftrightarrow x=1\pm\sqrt{5}\)

3.

ĐK: \(x\ge-9\)

\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)

\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)

\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)

Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)

\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)

\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)

\(\Leftrightarrow...\)

2.

ĐK: \(x\ne\dfrac{2\pm\sqrt{2}}{2};x\ne\dfrac{-2\pm\sqrt{2}}{2}\)

\(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{1}{2x+\dfrac{1}{x}+4}+\dfrac{1}{2x+\dfrac{1}{x}-4}=\dfrac{3}{5}\)

Đặt \(2x+\dfrac{1}{x}+4=a;2x+\dfrac{1}{x}-4=b\left(a,b\ne0\right)\)

\(pt\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{5}\left(1\right)\)

Lại có \(a-b=8\Rightarrow a=b+8\), khi đó:

\(\left(1\right)\Leftrightarrow\dfrac{1}{b+8}+\dfrac{1}{b}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{2b+8}{\left(b+8\right)b}=\dfrac{3}{5}\)

\(\Leftrightarrow10b+40=3\left(b+8\right)b\)

\(\Leftrightarrow\left[{}\begin{matrix}b=2\\b=-\dfrac{20}{3}\end{matrix}\right.\)

TH1: \(b=2\Leftrightarrow...\)

TH2: \(b=-\dfrac{20}{3}\Leftrightarrow...\)

a,sửa đề :  \(\left(\frac{1}{x^2+4x+4}-\frac{1}{x^2-4x+4}\right):\left(\frac{1}{x+2}+\frac{1}{x^2-4}\right)\)

\(=\left(\frac{1}{\left(x+2\right)^2}-\frac{1}{\left(x-2\right)^2}\right):\left(\frac{x-2+1}{\left(x+2\right)\left(x-2\right)}\right)\)

\(=\left(\frac{x^2-4x+4-x^2-4x-4}{\left(x+2\right)^2\left(x-2\right)^2}\right):\left(\frac{x-1}{\left(x+2\right)\left(x-2\right)}\right)\)

\(=\frac{-8x\left(x+2\right)\left(x-2\right)}{\left(x+2\right)^2\left(x-2\right)^2\left(x-1\right)}=\frac{-8x}{\left(x-1\right)\left(x^2-4\right)}\)

b, \(\left(\frac{2x}{2x-y}-\frac{4x^2}{4x^2+4xy+y^2}\right):\left(\frac{2x}{4x^2-y^2}+\frac{1}{y-2x}\right)\)

\(=\left(\frac{2x}{2x-y}-\frac{4x^2}{\left(2x+y\right)^2}\right):\left(\frac{2x}{\left(2x-y\right)\left(2x+y\right)}-\frac{1}{2x-y}\right)\)

\(=\left(\frac{2x\left(2x+y\right)^2-4x^2\left(2x-y\right)}{\left(2x-y\right)\left(2x+y\right)^2}\right):\left(\frac{2x-\left(2x+y\right)}{\left(2x-y\right)\left(2x+y\right)}\right)\)

\(=\left(\frac{8x^3+8x^2y+2xy^2-8x^3+4x^2y}{\left(2x-y\right)\left(2x+y\right)^2}\right):\left(\frac{-y}{\left(2x-y\right)\left(2x+y\right)}\right)\)

\(=-\left(\frac{12x^2y+xy^2}{2x+y}\right)=\frac{-12x^2y-xy^2}{2x+y}\)

\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)

\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\) 

Từ đó ta có đồ thị hàm số như sau:

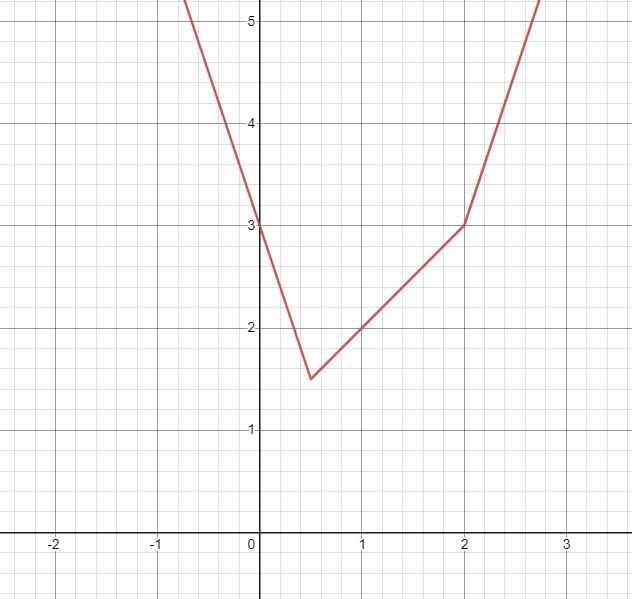
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):

- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)

- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)

- Vô nghiệm khi \(m< \dfrac{3}{2}\)

1. \(\sqrt{x^2-4x+3}=x-2\)

<=> x² - 4x + 3 = (x - 2)²

<=> x² - 4x + 3 = x² - 4x + 4

<=> x² - x² - 4x + 4x = 1

<=> 0 = 1 (Vô lí)

vậy PT có nghiệm là S = \(\varnothing\)

2. \(\sqrt{4x^2-4x+1}=x-1\)

<=> \(\sqrt{\left(2x-1\right)^2}=x-1\)

<=> 2x - 1 = x - 1

<=> 2x - x = -1 + 1

<=> x = 0

1: ta có: \(\sqrt{x^2-4x+3}=x-2\)

\(\Leftrightarrow x^2-4x+3=x^2-4x+4\)(vô lý)

2: Ta có: \(\sqrt{4x^2-4x+1}=x-1\)

\(\Leftrightarrow\left(2x-1-x+1\right)\left(2x-1+x-1\right)=0\)

\(\Leftrightarrow x\left(3x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)

Đề bài yêu cầu j?

\(=\sqrt{4x-1-2\sqrt{4x-1}+1}+\sqrt{4x-1+2\sqrt{4x-1}+1}\)

\(=\sqrt{\left(\sqrt{4x-1}-1\right)^2}+\sqrt{\left(\sqrt{4x-1}+1\right)^2}\)

\(=\left|\sqrt{4x-1}-1\right|+\sqrt{4x-1}+1\)

\(=\left[{}\begin{matrix}2\sqrt{4x-1}\text{ nếu }x\ge\dfrac{1}{2}\\2\text{ nếu }\dfrac{1}{4}\le x< \dfrac{1}{2}\end{matrix}\right.\)

a: Ta có: \(\left(3x-1\right)^2-\left(3x+4\right)\left(3x-4\right)=32\)

\(\Leftrightarrow9x^2-6x+1-9x^2+16=32\)

\(\Leftrightarrow-6x=15\)

hay \(x=-\dfrac{5}{2}\)

b: Ta có: \(\left(4x+3\right)^2-\left(4x-1\right)\left(4x+1\right)=-14\)

\(\Leftrightarrow16x^2+24x+9-16x^2+1=-14\)

\(\Leftrightarrow24x=-24\)

hay x=-1

a) \(\sqrt[]{x^2-2x+4}=2x-2\)

\(\Leftrightarrow\sqrt[]{x^2-2x+4}=2\left(x-1\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x-1\right)\ge0\\x^2-2x+4=4\left(x-1\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x^2-2x+4=4x^2-8x+4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\3x^2-6x=0\end{matrix}\right.\) \(\left(1\right)\)

Giải pt \(3x^2-6x=0\)

\(\Leftrightarrow3x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=2\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow x=2\)

c) \(\sqrt{x^2-3x+2}=\sqrt[]{x-1}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x^2-3x+2=x-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x^2-4x+3=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x=1\cup x=3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

1: =>x^2-x=3-x

=>x^2=3

=>x=căn 3 hoặc x=-căn 3

2: =>x^2-4x+3=x^2-4x+4 và x>=2

=>3=4(vô lý)

3: =>2|x-1|=6

=>|x-1|=3

=>x-1=3 hoặc x-1=-3

=>x=-2 hoặc x=4

4: =>|2x-3|=|x-2|

=>2x-3=x-2 hoặc 2x-3=-x+2

=>x=1 hoặc x=5/3

5: =>\(\sqrt{x+2}\left(\sqrt{x-2}+\sqrt{x+2}\right)=0\)

=>x+2=0

=>x=-2