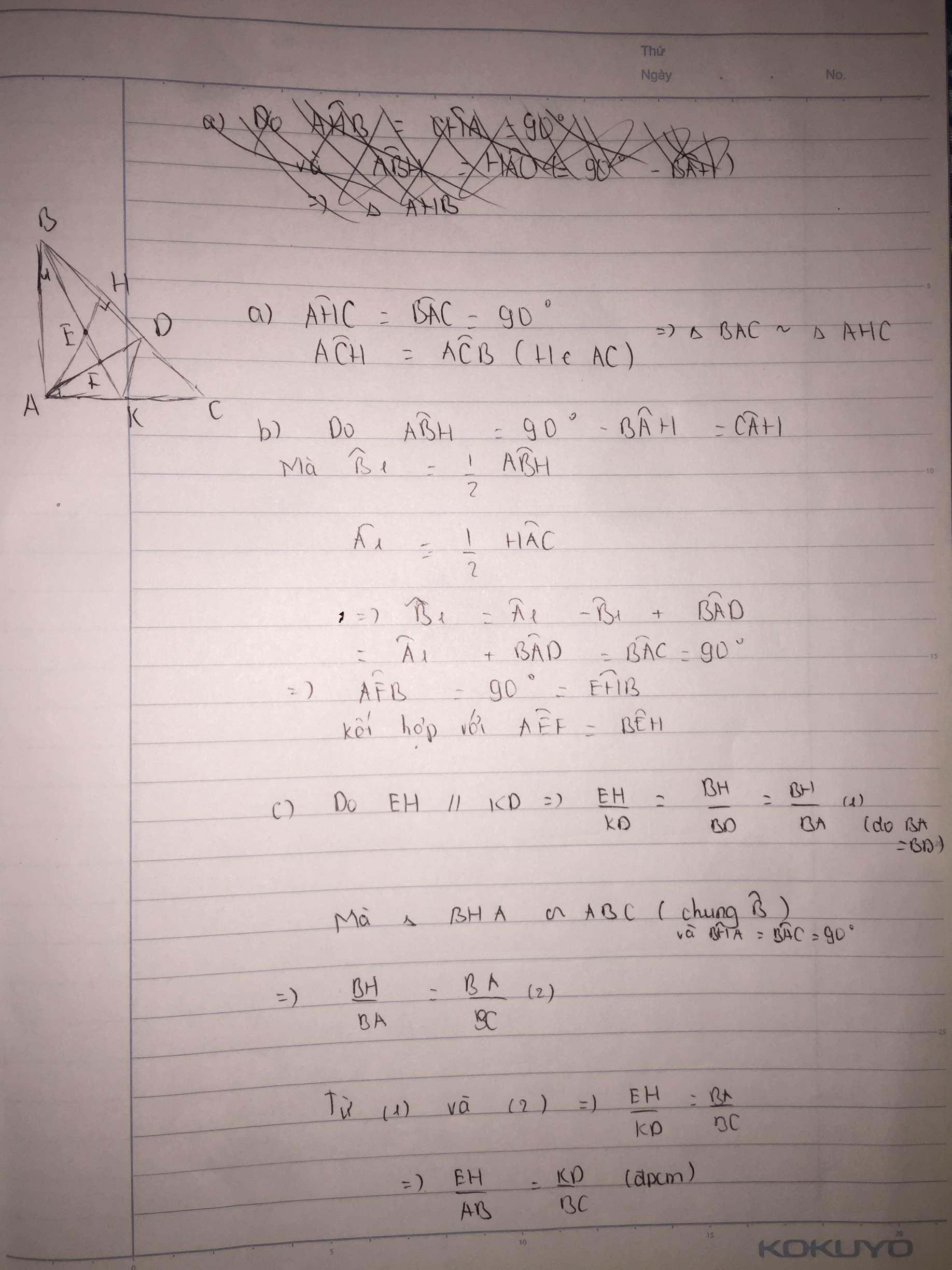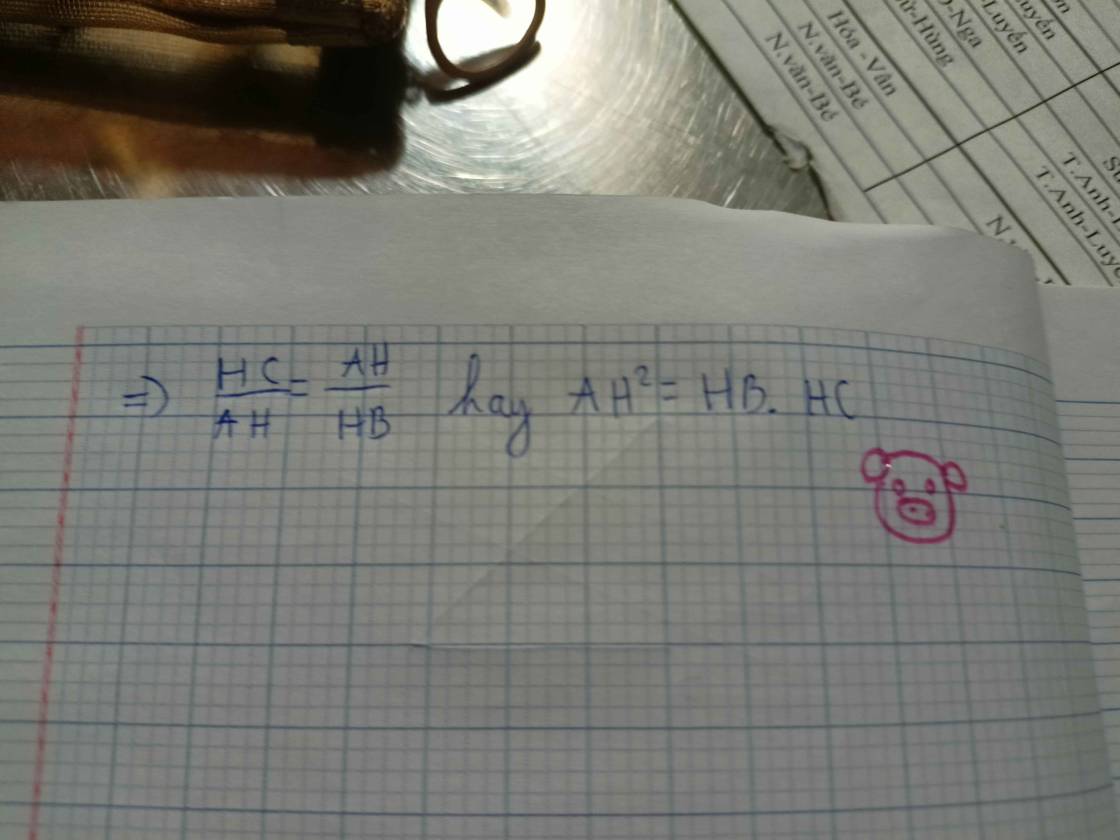Bài 3: Cho \(\Delta ABC\) vuông tại A, đường cao AH
a. Chứng minh \(\Delta AHB\) đồng dạng với \(\Delta CBA\)
b. Kẻ đường phân giác AD của \(\Delta CAH\) và đường phân giác BK của \(\Delta ABC\) \(\left(D\in BC,K\in AC\right)\), BK cắt AH và AD lần lượt tại E và F. Chứng minh \(\Delta AEF\) đồng dạng với \(\Delta BEH\)
c Chứng minh: KD // AH. Chứng minh \(\dfrac{EH}{AB}=\dfrac{KD}{BC}\)