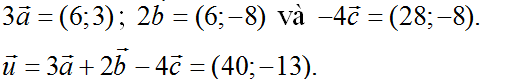Cho \(\overrightarrow{a}\)=(4;-m) , \(\overrightarrow{b}\)=(2m+6;1). Tìm m để hai vecto cùng phương

Những câu hỏi liên quan
Cho ba véc-tơ overrightarrow{a},overrightarrow{b},overrightarrow{c}thỏa mãn:|overrightarrow{a}| 4, |overrightarrow{b} |1, |overrightarrow{c}| 5 và 5(overrightarrow{b}-overrightarrow{a} ) + 3overrightarrow{c}overrightarrow{0}.Khi đó biểu thức M overrightarrow{a}.overrightarrow{b}+overrightarrow{b}.overrightarrow{c}+overrightarrow{c}.overrightarrow{a} có giá trị là bao nhiêu
Đọc tiếp
Cho ba véc-tơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)thỏa mãn:
|\(\overrightarrow{a}\)| = 4, |\(\overrightarrow{b}\) |=1, |\(\overrightarrow{c}\)| = 5 và 5(\(\overrightarrow{b}-\overrightarrow{a}\) ) + 3\(\overrightarrow{c}\)=\(\overrightarrow{0}\).
Khi đó biểu thức M = \(\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}.\overrightarrow{c}+\overrightarrow{c}.\overrightarrow{a}\) có giá trị là bao nhiêu
Cho hai vecto overrightarrow{a};overrightarrow{b} khác vecto 0. left|overrightarrow{a}right|4;left|overrightarrow{b}right|3;left|overrightarrow{a}-overrightarrow{b}right|4. Gọi alpha là góc giữa hai vecto a vầ b. Chọn phát biểu đúngA. alpha 60 độ B. alpha 30 độ C. cosalphadfrac{1}{3} Dcosalphadfrac{3}{8}
Đọc tiếp
Cho hai vecto \(\overrightarrow{a};\overrightarrow{b}\) khác vecto 0. \(\left|\overrightarrow{a}\right|=4;\left|\overrightarrow{b}\right|=3;\left|\overrightarrow{a}-\overrightarrow{b}\right|=4\). Gọi \(\alpha\) là góc giữa hai vecto a vầ b. Chọn phát biểu đúng
A. \(\alpha\)= 60 độ B. \(\alpha\)= 30 độ C. \(\cos\alpha=\dfrac{1}{3}\) D\(\cos\alpha=\dfrac{3}{8}\)
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=4\)
⇒ \(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=16\)
⇒ 16 + 9 - 2\(\overrightarrow{a}.\overrightarrow{b}\) = 16
⇒ \(2\overrightarrow{a}.\overrightarrow{b}=9\)
⇒ cosα = \(\dfrac{9}{2.4.3}\)
⇒ cos α = \(\dfrac{3}{8}\)
Vậy chọn D
Đúng 2
Bình luận (0)
Cho tam giác ABC đều cạnh a. M và N là các điểm sao cho 3overrightarrow{BM} 2overrightarrow{BC}, 5overrightarrow{AN} 4overrightarrow{AC}a, tính overrightarrow{AB}.overrightarrow{AC}; overrightarrow{BC}.overrightarrow{AC}b, cm AM vuông góc BN
Đọc tiếp
Cho tam giác ABC đều cạnh a. M và N là các điểm sao cho 3\(\overrightarrow{BM}\)= 2\(\overrightarrow{BC}\), 5\(\overrightarrow{AN}\) = 4\(\overrightarrow{AC}\)
a, tính \(\overrightarrow{AB}\).\(\overrightarrow{AC}\); \(\overrightarrow{BC}\).\(\overrightarrow{AC}\)
b, cm AM vuông góc BN
Cho overrightarrow{a}left(2;1right);overrightarrow{b}left(3;-4right);overrightarrow{c}left(-7;2right)
a) Tìm tọa độ của vectơ overrightarrow{u}3overrightarrow{a}+2overrightarrow{b}-4overrightarrow{c}
b) Tìm tọa độ vectơ overrightarrow{x} sao cho : overrightarrow{x}+overrightarrow{a}overrightarrow{b}-overrightarrow{c}
c) Tìm các số k và h sao cho : overrightarrow{c}koverrightarrow{a}+hoverrightarrow{b}
Đọc tiếp
Cho \(\overrightarrow{a}=\left(2;1\right);\overrightarrow{b}=\left(3;-4\right);\overrightarrow{c=}\left(-7;2\right)\)
a) Tìm tọa độ của vectơ \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}\)
b) Tìm tọa độ vectơ \(\overrightarrow{x}\) sao cho : \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\)
c) Tìm các số k và h sao cho : \(\overrightarrow{c}=k\overrightarrow{a}+h\overrightarrow{b}\)
a) \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}=3\left(2;1\right)+2\left(3;-4\right)-4\left(-7;2\right)\)
\(=\left(6;3\right)+\left(6;-8\right)-\left(-28;8\right)\)
\(=\left(6+6+28;3-8-8\right)=\left(40;-13\right)\).
b) \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\Leftrightarrow\overrightarrow{x}=\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{a}\)
\(\Leftrightarrow\overrightarrow{x}=\left(3;-4\right)-\left(-7;2\right)-\left(2;1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(3+7-2;-4-2-1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(8;-7\right)\).
c) Có \(\overrightarrow{c}\left(-7;2\right)=k\overrightarrow{a}+h\overrightarrow{b}=k\left(2;1\right)+h\left(3;-4\right)\)
\(=\left(2k+3h;k-4h\right)\).
Từ đó suy ra: \(\left\{{}\begin{matrix}2k+3h=-7\\k-4h=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}k=-2\\h=-1\end{matrix}\right.\).
Đúng 0
Bình luận (0)
Cho overrightarrow{a}left(2;1right);overrightarrow{b}left(3;-4right);overrightarrow{c}left(-7;2right)
a) Tìm tọa độ của vectơ overrightarrow{u}3overrightarrow{a}+2overrightarrow{b}-4overrightarrow{c}
b) Tìm tọa độ của vectơ overrightarrow{x} sao cho overrightarrow{x}+overrightarrow{a}overrightarrow{b}-overrightarrow{c}
c) Tìm các số k và h sao cho overrightarrow{c}koverrightarrow{a}+hoverrightarrow{b}
Đọc tiếp
Cho \(\overrightarrow{a}=\left(2;1\right);\overrightarrow{b}=\left(3;-4\right);\overrightarrow{c}=\left(-7;2\right)\)
a) Tìm tọa độ của vectơ \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}\)
b) Tìm tọa độ của vectơ \(\overrightarrow{x}\) sao cho \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\)
c) Tìm các số k và h sao cho \(\overrightarrow{c}=k\overrightarrow{a}+h\overrightarrow{b}\)
Câu 1: Trong hệ trục (O,overrightarrow{i},overrightarrow{j}), tọa độ overrightarrow{i}-overrightarrow{j}làCâu 2:Cho overrightarrow{a}(3;-4), overrightarrow{b}(-1;2). Tọa độ vecto overrightarrow{a}+2overrightarrow{b}là
Đọc tiếp
Câu 1: Trong hệ trục (O,\(\overrightarrow{i}\),\(\overrightarrow{j}\)), tọa độ \(\overrightarrow{i}\)-\(\overrightarrow{j}\)là
Câu 2:Cho \(\overrightarrow{a}\)(3;-4), \(\overrightarrow{b}\)(-1;2). Tọa độ vecto \(\overrightarrow{a}\)+2\(\overrightarrow{b}\)là
Lời giải:
$\overrightarrow{i}=(1,0), \overrightarrow{j}=(0,1)$
$\Rightarrow \overrightarrow{i}-\overrightarrow{j}=(1-0,0-1)=(1,-1)$
Đúng 1
Bình luận (0)
Bài 2:
$\overrightarrow{a}+2\overrightarrow{b}=(3+2.-1, -4+2.2)=(1, 0)$
Đúng 1
Bình luận (0)
Trong hệ trục tọa độ Oxy,cho các vecto \(\overrightarrow{a}\) =(2;3), \(\overrightarrow{b}\)=(1;-4)và \(\overrightarrow{c}\)=(5;12). Tìm cặp số x, y sao cho \(\overrightarrow{c}=x.\overrightarrow{a}+y.\overrightarrow{b}\)
Help me!!!
\(\Leftrightarrow\left\{{}\begin{matrix}5=2x+1.y\\12=3.x-4.y\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{32}{11}\\y=-\dfrac{9}{11}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1. Cho overrightarrow{x} (Độ dài overrightarrow{x} là 4 ô vở). Hãy dựng các vecto sau :a) 2.overrightarrow{x}b) - 0,5 overrightarrow{x}c) dfrac{3}{4}overrightarrow{x}d) dfrac{5}{4}overrightarrow{x}e) - dfrac{1}{4}overrightarrow{x}
Đọc tiếp
1. Cho \(\overrightarrow{x}\) (Độ dài \(\overrightarrow{x}\) là 4 ô vở). Hãy dựng các vecto sau :
a) 2.\(\overrightarrow{x}\)
b) - 0,5 \(\overrightarrow{x}\)
c) \(\dfrac{3}{4}\)\(\overrightarrow{x}\)
d) \(\dfrac{5}{4}\)\(\overrightarrow{x}\)
e) - \(\dfrac{1}{4}\)\(\overrightarrow{x}\)
Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow{a}=2\overrightarrow{i}\) , \(\overrightarrow{b}=-3\overrightarrow{j}\), \(\overrightarrow{c}=3\overrightarrow{i}-4\overrightarrow{j}\)
Phân tích vecto c theo hai vecto a và vecto b
Giả sử `\vec{c}=m\vec{a}+n\vec{b}`
`<=>(3;-4)=m(2;0)+n(0;-3)`
`<=>(3;-4)=(2m;-3n)`
`<=>{(m=3/2),(n=4/3):}`
`=>\vec{c}=3/2\vec{a}+4/3\vec{b}`
Đúng 2
Bình luận (0)
Cho hai vectơ \(\overrightarrow m = \left( { - 6;1} \right),\overrightarrow n = \left( {0;2} \right)\)
a) Tìm tọa độ các vectơ \(\overrightarrow m + \overrightarrow n ,\overrightarrow m - \overrightarrow n ,10\overrightarrow m , - 4\overrightarrow n \)
b) Tính các tích vô hướng \(\overrightarrow m .\overrightarrow n ,\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right)\)
a) Ta có
\(\begin{array}{l}\overrightarrow m + \overrightarrow n = \left( {\left( { - 6 + 0} \right);1 + 2} \right) = ( - 6;3)\\\overrightarrow m - \overrightarrow n = \left( {\left( { - 6 - 0} \right);\left( {1 - 2} \right)} \right) = \left( { - 6; - 1} \right)\\10\overrightarrow m = (10.( - 6);10.1) = ( - 60;10)\\ - 4\overrightarrow n = (( - 4).0;( - 4).2) = (0; - 8)\end{array}\)
b) Ta có
\(\overrightarrow m .\overrightarrow n = ( - 6).0 + 1.2 = 0 + 2 = 2\)
Ta có \(10\overrightarrow m = ( - 60;10)\) và \( - 4\overrightarrow n = (0; - 8)\) nên \(\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right) = ( - 60).0 + 10.( - 8) = 0 - 80 = - 80\)
Đúng 0
Bình luận (0)