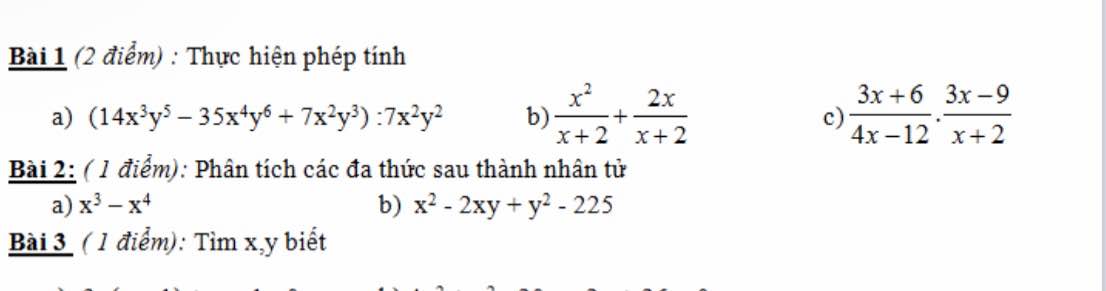Bài 65. Cho hình thang ABCD, đáy lớn AB. Gọi O là giao điểm AC và BD, đường thẳng qua 0 và song song với AB cắt AD, BC lượt tại M, N N. Chứng minh O là trung điểm của đoạn thẳng MN mọi người giúp mình nha, mình cảm ơn
Xem chi tiết
Bài 6: Diện tích đa giác
Cho hình chữ nhật ABCD có S=200cm^2.Tính S tam giác ABD
\(S_{ABD}=\dfrac{1}{2}S_{ABCD}=100\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác COE có các đường trung tuyến CM và EN cắt nhau tại G. I là trung điểm GO, K là trung điểm GE.
Chứng minh rằng tứ giác MNIK là hình bình hành
Sửa đề: Trung tuyến OM
Xét ΔCOE cso
N là trung điểm của CO
M là trung điểm của CE
Do đó: NM là đường trung bình của ΔCOE
Suy ra: NM//OE và NM=OE/2(1)
Xét ΔGOE có
I là trung điểm của GO
K là trung điểm của GE
Do đó: IK là đường trung bình của ΔGOE
Suy ra: IK//OE và IK=OE/2(2)
Từ (1) và (2) suy ra NM//IK và NM=IK
hay NMKI là hình bình hành
Đúng 0
Bình luận (0)
29 tháng 11 2021 lúc 19:53
cứu vs
Cho hình thang ABCD (AB // Cd) có AD= 6cm, góc D=450. Tính diện tích tứ giác có các ddirnhr là trung điểm của AB, AD, CD, BD.
Cho hình vuông có cạnh bằng 15cm. Trên cạnh AB lấy điểm M sao cho diện tích
tam giác AMD bằng 1/3 diện tích hình vuông ABCD
Yêu cầu đề bài là gì vậy bạn? Nếu là tìm diện tích tam giác $AMD$ thì:
$S_{AMD}=\frac{1}{3}S_{ABCD}=\frac{1}{3}.15.15=75$ (cm2)
Đúng 0
Bình luận (0)
Tính chu vi của hcn biết tỉ số giữa hai cạnh của nó là ở và diện tích của hơn là 135 cm.
Đề thiếu tỉ số giữa hai cạnh. Bạn coi lại.
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Từ A và C kẻ AE và CF vuông góc với BD tại E và F.
a) Chứng minh 2 đa giác ABCFE và ADCFE có diện tích bằng nhau
b) Tính diện tích của hai đa giác nói trên nếu các cạnh của hơn tỉ lệ với 4 và 3. Chu vi của hơn là 56cm.
Tính chu vi của hcn biết tỉ số giữa hai cạnh của nó là 3/5 ở và diện tích của hơn là 135 cm.
Cho tam giác ABC vuông tại A, AF = 1,62cm; HC = 2,5cm, GC = 2cm, BD = 1,5cm;
BA = 3,7 cm. Biết tam giác BDE đều, HG vuông góc với GC, tính diện tích đa giác DEGHF.
Bài 2:
a: \(=x^3\left(1-x\right)\)
b: \(=\left(x-y\right)^2-225=\left(x-y-15\right)\left(x-y+15\right)\)
Đúng 0
Bình luận (0)