Giúp mình nhanh với .Trong mp tọa độ Oxy cho điểm A (1;0) và đường thẳng (d):x+y-2=0. Tìm ảnh của A và(d) qua phép quay Q(O;90°)
Bài 5: Phép quay
Giúp mình giải Trong mp tọa độ Oxy cho điểm A(0;3) tìm B=Q(0 -45°)
Giúp mik nhanh với trong mp Oxg cho phép quay Q(0;45) tìm ảnh của a Điểm B (2;2) .b Đường tròn (C) (x-1)^2+y^2=4
1. Cho 2 Δđều OAB & ΔOA′B′. Gọi C, D lần lượt là trung điểm của AA, BB. CM ΔOCD đều2. Cho 2 Δ vuông cân OAB và OAB chung đỉnh O sao cho O nằm trên đoạn thẳng AB và nằm ngoài đường thẳng AB. Gọi G, G lần lượt là trọng tâm ΔOAA′,ΔOBB′. CM ΔGOG′ vuông cân
Đọc tiếp
1. Cho 2 Δđều OAB & ΔOA′B′. Gọi C, D lần lượt là trung điểm của AA', BB'. CM ΔOCD đều
2. Cho 2 Δ vuông cân OAB và OA'B' chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đường thẳng A'B. Gọi G, G' lần lượt là trọng tâm ΔOAA′,ΔOBB′. CM ΔGOG′ vuông cân
Cho đường thẳng d: x-y+3=0, tìm ảnh của d qua Q(0;30°)
tìm ảnh của d:2x+3y+4=0 qua phép quay Q(I;450) biết I(2;1)
Gọi \(M\left(x;y\right)\) là 1 điểm bất kì thuộc d \(\Rightarrow2x+3y+4=0\Leftrightarrow2.2x+3.2y+8=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép quay Q
\(\Rightarrow M'\in d'\) với d' là ảnh của d qua phép quay Q
Ta có: \(\left\{{}\begin{matrix}x'=2+\left(x-2\right)cos45^0-\left(y-1\right)sin45^0\\y'=1+\left(x-2\right)sin45^0+\left(y-1\right)cos45^0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=\sqrt{2}x'-2\sqrt{2}+1\\x+y=\sqrt{2}y'-\sqrt{2}+3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=\sqrt{2}\left(x'+y'\right)-3\sqrt{2}+4\\2y=\sqrt{2}\left(y'-x'\right)+\sqrt{2}+2\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow2\sqrt{2}\left(x'+y'\right)-6\sqrt{2}+8+3\sqrt{2}\left(y'-x'\right)+3\sqrt{2}+6+8=0\)
\(\Leftrightarrow-\sqrt{2}x'+5\sqrt{2}y'+22-3\sqrt{2}=0\)
\(\Leftrightarrow x'-5y'+3-11\sqrt{2}=0\)
Hay pt d' có dạng: \(x-5y+3-11\sqrt{2}=0\)
Đúng 2
Bình luận (0)
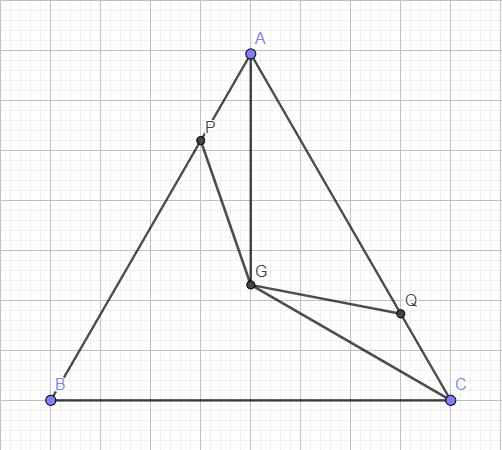
Giải giúp e vs ạ
Gọi G là trọng tâm tam giác \(\Rightarrow\) G cố định
Do tam giác ABC đều \(\Rightarrow\widehat{GAB}=\widehat{GAC}=\dfrac{1}{2}.60^0=30^0\)
Đồng thời \(\widehat{AGC}=\dfrac{1}{3}.360^0=120^0\)
Xét 2 tam giác GAP và GCQ có: \(\left\{{}\begin{matrix}AP=CQ\\\widehat{GAB}=\widehat{GAC}\\AG=CG\end{matrix}\right.\) \(\Rightarrow\Delta GAP=\Delta GCQ\)
\(\Rightarrow\left\{{}\begin{matrix}GP=GQ\\\widehat{PGA}=\widehat{QGC}\Rightarrow\widehat{PGQ}=\widehat{AGC}=120^0\end{matrix}\right.\)
\(\Rightarrow\) Q là ảnh của P qua phép quay tâm G góc 120 độ, C là ảnh của A qua phép quay tâm G góc 120 độ
\(\Rightarrow Q_{\left(G;120^0\right)}\left(\overrightarrow{AP}\right)=\overrightarrow{CQ}\)
b. Theo cmt, do \(\Delta GAP=\Delta GCQ\Rightarrow\widehat{GPA}=\widehat{GQC}\)
Mà \(\widehat{GQC}+\widehat{GQA}=180^0\Rightarrow\widehat{GPA}+\widehat{GQA}=180^0\)
\(\Rightarrow\) Tứ giác APGQ nội tiếp hay đường tròn (APQ) luôn đi qua G cố định
Đúng 1
Bình luận (0)