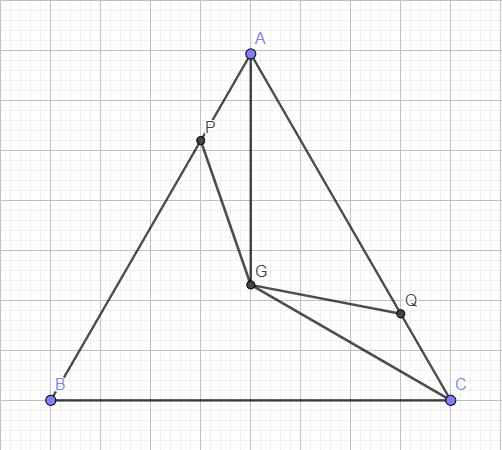
Gọi G là trọng tâm tam giác \(\Rightarrow\) G cố định
Do tam giác ABC đều \(\Rightarrow\widehat{GAB}=\widehat{GAC}=\dfrac{1}{2}.60^0=30^0\)
Đồng thời \(\widehat{AGC}=\dfrac{1}{3}.360^0=120^0\)
Xét 2 tam giác GAP và GCQ có: \(\left\{{}\begin{matrix}AP=CQ\\\widehat{GAB}=\widehat{GAC}\\AG=CG\end{matrix}\right.\) \(\Rightarrow\Delta GAP=\Delta GCQ\)
\(\Rightarrow\left\{{}\begin{matrix}GP=GQ\\\widehat{PGA}=\widehat{QGC}\Rightarrow\widehat{PGQ}=\widehat{AGC}=120^0\end{matrix}\right.\)
\(\Rightarrow\) Q là ảnh của P qua phép quay tâm G góc 120 độ, C là ảnh của A qua phép quay tâm G góc 120 độ
\(\Rightarrow Q_{\left(G;120^0\right)}\left(\overrightarrow{AP}\right)=\overrightarrow{CQ}\)
b. Theo cmt, do \(\Delta GAP=\Delta GCQ\Rightarrow\widehat{GPA}=\widehat{GQC}\)
Mà \(\widehat{GQC}+\widehat{GQA}=180^0\Rightarrow\widehat{GPA}+\widehat{GQA}=180^0\)
\(\Rightarrow\) Tứ giác APGQ nội tiếp hay đường tròn (APQ) luôn đi qua G cố định