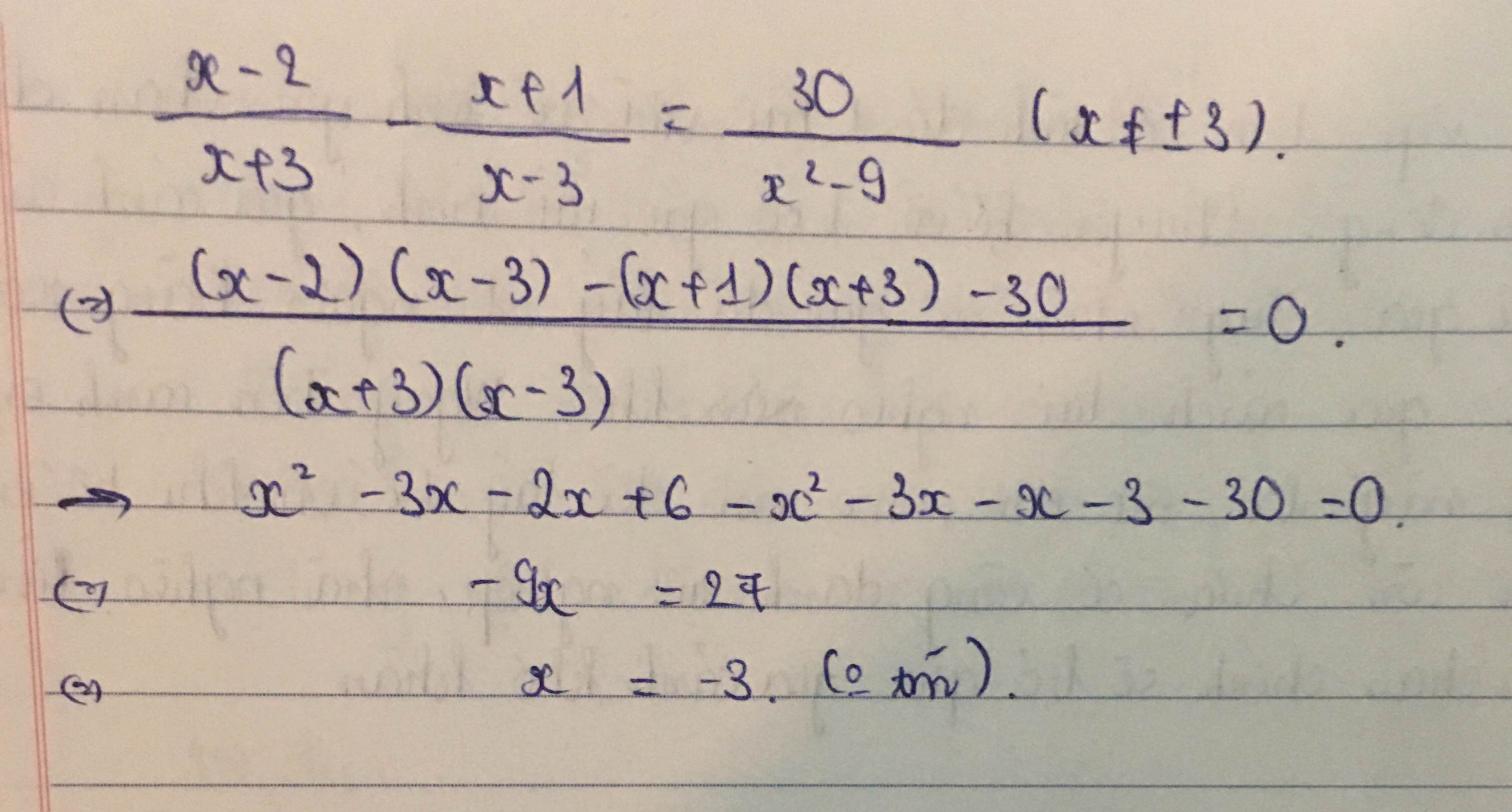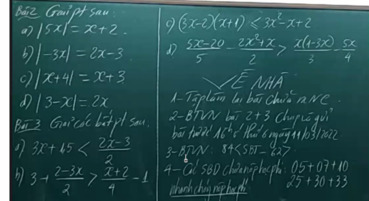Bài 1: Mở đầu về phương trình
\(\dfrac{x-2}{x+3}-\dfrac{x+1}{x-3}=\dfrac{30}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{x-2}{x+3}-\dfrac{x+1}{x-3}=\dfrac{30}{\left(x+3\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{30}{\left(x+3\right)\left(x-3\right)}\)
\(\Rightarrow x^2-3x-2x+6-\left(x^2+3x+x+3\right)=30\)
\(\Leftrightarrow x^2-3x-2x+6-x^2-3x-x-3=30\)
\(\Leftrightarrow-9x+3=30\)
\(\Leftrightarrow-9x-27=0\)
\(\Leftrightarrow x=-3\left(loại\right)\)
-Vậy S=∅
Đúng 1
Bình luận (0)
Bài 2
a, đk : x > = -2
\(\left[{}\begin{matrix}5x=x+2\\5x=-x-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-\dfrac{1}{3}\end{matrix}\right.\left(tm\right)\)
b, đk : x > = 3/2
\(\left[{}\begin{matrix}-3x=2x-3\\-3x=3-2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\left(ktm\right)\\x=-3\left(ktm\right)\end{matrix}\right.\)
c, đk : x > = - 3
\(\left[{}\begin{matrix}x+4=x+3\\x+4=-x-3\end{matrix}\right.\Leftrightarrow2x=1\Leftrightarrow x=\dfrac{1}{2}\)(tm)
d, đk : x > = 0 \(\left[{}\begin{matrix}3-x=2x\\3-x=-2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-3\left(ktm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
x+1/4-x-7/3=1
=>3(x+1)-4(x-7)=12
=>3x+3-4x+28=12
=>31-x=12
hay x=19
Đúng 0
Bình luận (0)
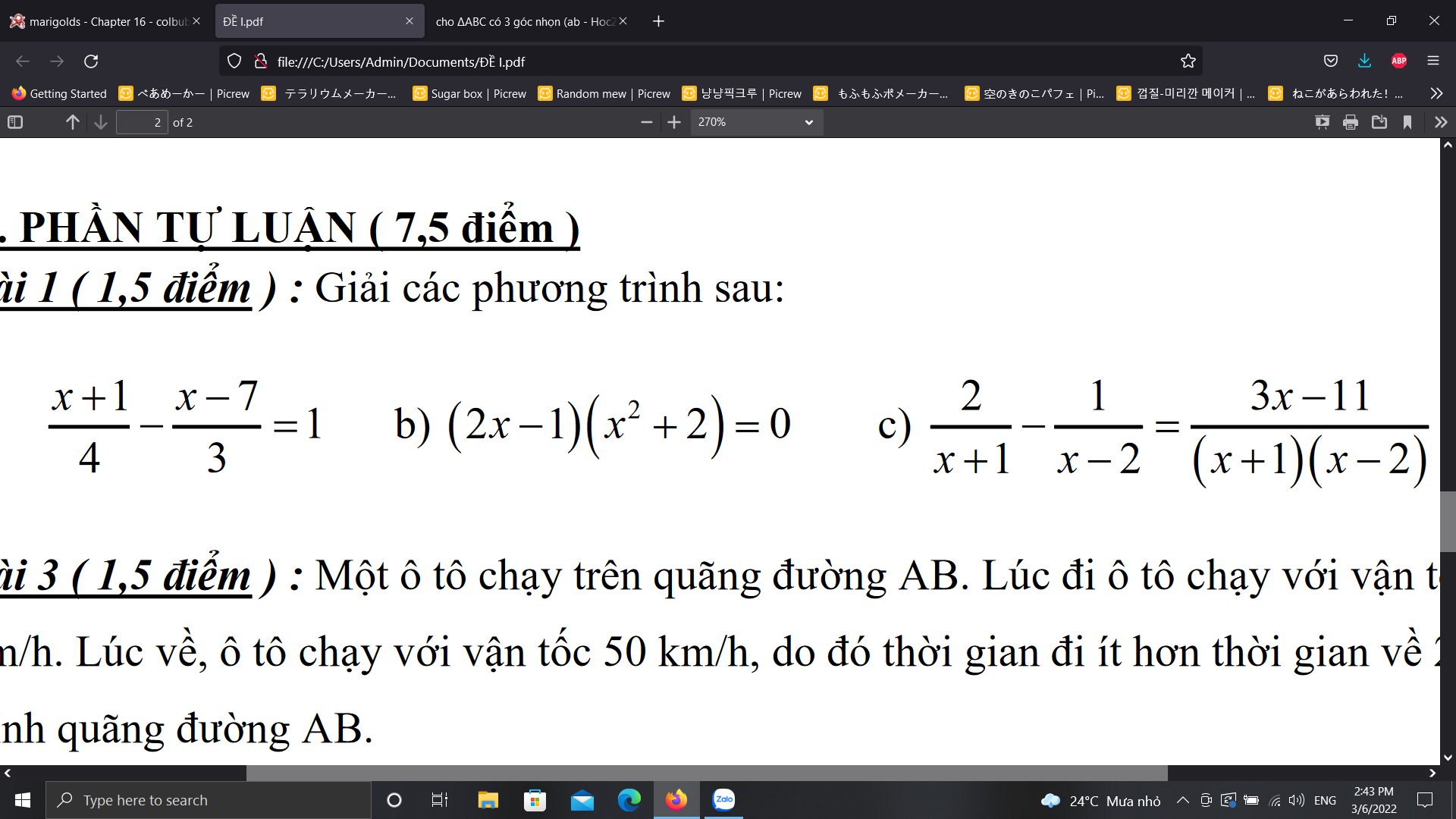
Bài 1:
a: =>3(x+1)-4(x-7)=12
=>3x+3-4x+28=12
=>31-x=12
hay x=19
b: =>2x-1=0
hay x=1/2
c: \(\Leftrightarrow2\left(x-2\right)-x-1=3x-11\)
=>2x-4-x-1=3x-11
=>3x-11=x-5
=>2x=6
hay x=3(nhận)
Đúng 0
Bình luận (0)
i, \(\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\)
k, \(\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\)
l, \(\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\)
\(\left(x-1\right)\left(-x+2\right)=0\Leftrightarrow x=1;x=2\)
\(\left(x+2\right)\left(x+1-x+3\right)=0\Leftrightarrow x=-2\)
\(\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(2x+5\right)=0\Leftrightarrow\left(x-2\right)\left(-x-2\right)=0\Leftrightarrow x=-2;x=2\)
Đúng 4
Bình luận (0)
\(i,\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(-x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\\ k,\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x+1-x+3\right)=0\\ \Leftrightarrow4\left(x+2\right)=0\\ \Leftrightarrow x+2=0\\ \Leftrightarrow x=-2\\ l,\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\\ \Leftrightarrow\left(x-2\right)\left(2x+5\right)-\left(x-2\right)\left(x+3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+5-x-3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
e, x2 (2x - 3) + 2(2x - 3)=0
g, 3x(x + 5) - 2x -10 =0
\(a,x^2\left(2x-3\right)+2\left(2x-3\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(x^2+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x^2+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x^2=-2\left(ktm\right)\end{matrix}\right.\)
\(b,3x\left(x+5\right)-2x-10=0\\ \Leftrightarrow b,3x\left(x+5\right)-2\left(x+5\right)=0\\ \Leftrightarrow\left(x+5\right)\left(3x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+5=0\\3x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{2}{3}\end{matrix}\right.\)
Đúng 6
Bình luận (1)
e) \(\left(2x-3\right)\left(x^2+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x^2=-2\left(ktm\right)\end{matrix}\right.\)
g) \(3x\left(x+5\right)-2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(3x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{2}{3}\end{matrix}\right.\)
Đúng 2
Bình luận (1)
\(\dfrac{2x}{3}+\dfrac{2x-1}{6}=4-\dfrac{x}{3}\)
\(4x+2x-1=24-2x\Leftrightarrow8x=25\Leftrightarrow x=\dfrac{25}{8}\)
Đúng 6
Bình luận (0)
\(\Leftrightarrow\dfrac{4x+2x-1}{6}=\dfrac{24-2x}{6}\)
\(\Leftrightarrow4x+2x-1=24-2x\)
\(\Leftrightarrow8x=25\)
\(\Leftrightarrow x=\dfrac{25}{8}\)
Đúng 5
Bình luận (0)
\(\dfrac{x}{3}-\dfrac{2x+1}{2}=\dfrac{x}{6}-x\)
\(\Leftrightarrow\dfrac{2x-3\left(2x+1\right)}{6}=\dfrac{x-6x}{6}\)
\(\Leftrightarrow2x-3\left(2x+1\right)=x-6x\)
\(\Leftrightarrow2x-6x-3+5x=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Đúng 3
Bình luận (1)
\(\Leftrightarrow\dfrac{2x}{6}-\dfrac{3\left(2x+1\right)}{6}=\dfrac{x}{6}-\dfrac{6x}{6}\)
\(\Leftrightarrow2x-3\left(2x+1\right)=x-6x\)
\(\Leftrightarrow2x-6x-3=x-6x\)
\(\Leftrightarrow2x-6x-x+6x=3\)
\(\Leftrightarrow x=3\)
Vậy : S = {3}
Đúng 1
Bình luận (0)
\(\dfrac{x}{3}-\dfrac{2x+1}{2}=\dfrac{x}{6}-x\)
\(\Leftrightarrow2x-3\left(2x+1\right)=x-6x\)
\(\Leftrightarrow2x-6x-3-x+6x=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
\(\dfrac{x+3}{2}-\dfrac{x-1}{3}=1+\dfrac{x+5}{6}\)
\(\dfrac{x+3}{2}-\dfrac{x-1}{3}=1+\dfrac{x+5}{6}\\ \Leftrightarrow\dfrac{3\left(x+3\right)}{6}-\dfrac{2\left(x-1\right)}{6}-\dfrac{6}{6}-\dfrac{x+5}{6}=0\\ \Leftrightarrow3x+9-2x+2-6-x-5=0\\ \Leftrightarrow0=0\left(luôn.đúng\right)\)
Vậy pt có vô số nghiệm
Đúng 5
Bình luận (0)
\(\Leftrightarrow\dfrac{3\left(x+3\right)-2\left(x-1\right)}{6}=\dfrac{6+\left(x+5\right)}{6}\)
\(\Leftrightarrow3\left(x+3\right)-2\left(x-1\right)=6+x+5\)
\(\Leftrightarrow3x+9-2x+2-11-x=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
Vậy \(x=R\)
Đúng 3
Bình luận (0)
\(\dfrac{x-1}{2}-\dfrac{2x-1}{12}=\dfrac{2-x}{4}-\dfrac{3x+2}{6}\)
B1: Quy đồng 2 vế
+) MTC: 12
B2: Khử mẫu
B3: Giải phương trình
~ Các bước làm đó bn, ko hiểu thì nói mình mình giải chi tiết cho nha ~
Đúng 1
Bình luận (0)
\(\dfrac{x-1}{2}-\dfrac{2x-1}{12}=\dfrac{2-x}{4}-\dfrac{3x+2}{6}\\ \Leftrightarrow\dfrac{6\left(x-1\right)}{12}-\dfrac{2x-1}{12}-\dfrac{3\left(2-x\right)}{12}-\dfrac{2\left(3x+2\right)}{12}=0\\ \Leftrightarrow6x-6-2x+1-6+3x-6x-4=0\\ \Leftrightarrow x-15=0\\ \Leftrightarrow x=15\)
Đúng 1
Bình luận (0)
\(6x-6-2x+1=6-3x-6x-4\Leftrightarrow4x-5=2-9x\)
\(\Leftrightarrow13x=7\Leftrightarrow x=\dfrac{7}{13}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời