Hàm số nào sau đây không là hàm số tuần hoàn? Giải thích?
tan2x; cosx+x; \(cot\left(x+\dfrac{\pi}{3}\right)\); sinx+1
Hàm số nào sau đây không là hàm số tuần hoàn? Giải thích?
tan2x; cosx+x; \(cot\left(x+\dfrac{\pi}{3}\right)\); sinx+1
Các hàm không tuần hoàn là cosx+x vì \(cosx+x\ne cos\left(x+k2\Omega\right)+x+k2\Omega\)
Tìm tập giá trị của hàm số: \(y=5+sin2023x\).
\(-1< =sin2023x< =1\)
=>\(-1+5< =5+sin2023x< =1+5\)
=>4<=y<=6
Vậy: TGT của hàm số là T=[4;6]
\(x\in\left(\Omega;\dfrac{3}{2}\Omega\right)\)
=>sin x đồng biến
=>1/sin x giảm
=>Mệnh đề (1) đúng
\(x\in\left(\Omega;\dfrac{3}{2}\Omega\right)\)
=>cosx đồng biến
=>1/cosx nghịch biến
=>Mệnh đề (2) đúng
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=sin\dfrac{2x}{x^2+1}+cos\dfrac{x}{x^2+1}+1\)
Cho 2tanα-cotα=1. Tính P=\(\dfrac{\text{tan ( 8 π − α ) + 2 cot ( π + α )}}{3\tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
2tan a-cot a=1
=>2tana-1/tan a=1
=>\(\dfrac{2tan^2a-1}{tana}=1\)
=>2tan^2a-tana-1=0
=>(tan a-1)(2tana+1)=0
=>tan a=-1/2 hoặc tan a=1
\(P=\dfrac{tan\left(-a\right)+2\cdot cota}{3\cdot tan\left(\dfrac{pi}{2}+a\right)}=\dfrac{-tana+2\cdot cota}{-3\cdot cota}\)
TH1: tan a=-1/2
\(P=\dfrac{\dfrac{1}{2}+2\cdot\left(-2\right)}{-3\cdot\left(-2\right)}=-\dfrac{7}{2}:6=-\dfrac{7}{12}\)
TH2: tan a=1
=>cot a=1
\(P=\dfrac{-1+2}{-3}=\dfrac{1}{-3}=-\dfrac{1}{3}\)
Ta có :
\(2tan\alpha-cot\alpha=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}-1=0\)
\(\Leftrightarrow\dfrac{2tan^2\alpha-tan\alpha-1}{tan\alpha}=0\left(tan\alpha\ne0\right)\)
\(\Leftrightarrow2tan^2\alpha-tan\alpha-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan\alpha=1\\tan\alpha=-\dfrac{1}{2}\end{matrix}\right.\)
\(P=\dfrac{tan\left(8\pi-\alpha\right)+2cot\left(\pi+\alpha\right)}{3tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(4.2\pi-\alpha\right)+2cot\alpha}{3tan\left(2\pi-\dfrac{\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(-\alpha\right)+2cot\alpha}{3tan\left[-\left(\dfrac{\pi}{2}-\alpha\right)\right]}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3tan\left(\dfrac{\pi}{2}-\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3cot\alpha}\)
- Với \(tan\alpha=1\Rightarrow cot\alpha=1\)
\(\Leftrightarrow P=\dfrac{-1+2.1}{-3.1}=-\dfrac{1}{3}\)
- Với \(tan\alpha=-\dfrac{1}{2}\Rightarrow cot\alpha=-2\)
\(\Leftrightarrow P=\dfrac{\dfrac{1}{2}+2.\left(-2\right)}{-3.\left(-2\right)}=\dfrac{-\dfrac{7}{2}}{6}=-\dfrac{7}{12}\)
Cho tanα = 2. Tính P=\(\dfrac{\tan\left(8\pi-\alpha\right)+2\cot\left(\pi+\alpha\right)}{3\tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
\(P=\dfrac{tan\left(-a\right)+2\cdot cota}{3\cdot tan\left(\dfrac{pi}{2}+a\right)}=\dfrac{-tana+2\cdot\dfrac{1}{2}}{3\cdot\left(-cota\right)}\)
\(=\dfrac{-2+1}{3\cdot\dfrac{-1}{2}}=-1:\dfrac{-3}{2}=\dfrac{2}{3}\)
Tìm TXĐ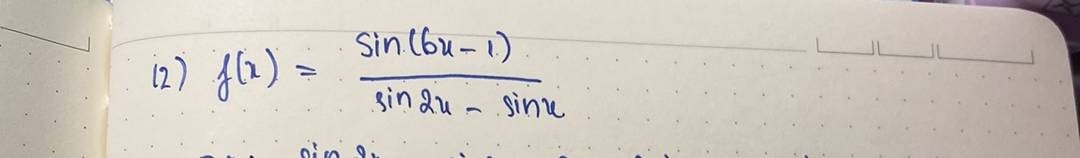
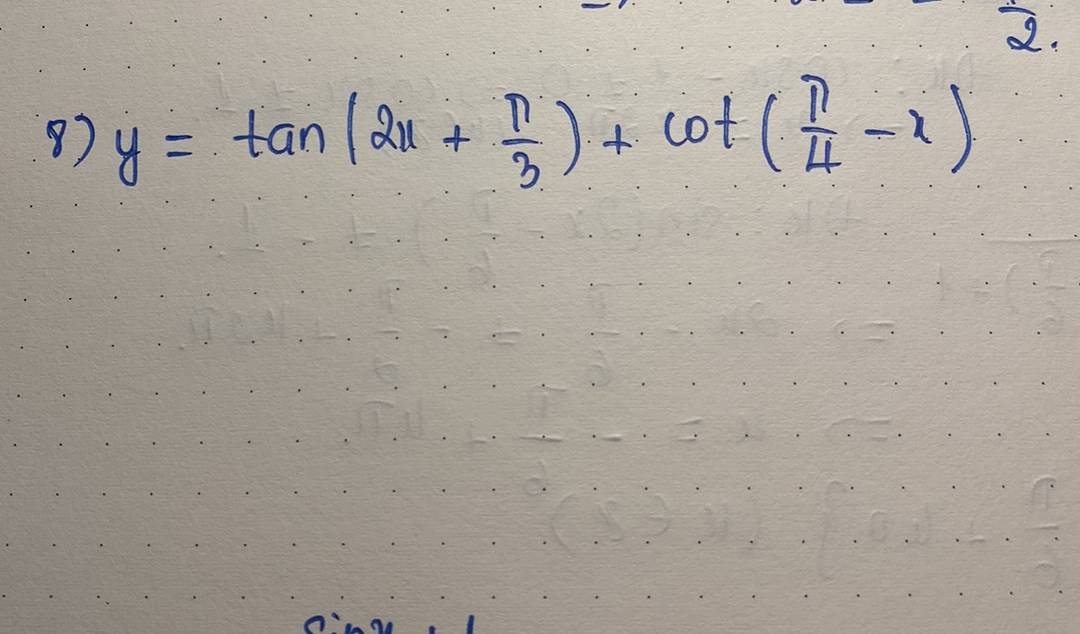
12: ĐKXĐ: sin 2x<>sin x
=>2x<>x+k2pi và 2x<>pi-x+k2pi
=>x<>k2pi và x<>pi/3+k2pi/3
Vậy: D=R\{k2pi;pi/3+k2pi/3}
8: ĐKXĐ: 2x+pi/3<>pi/2+kpi và pi/4-x<>kpi
=>2x<>pi/6+kpi và x<>pi/4-kpi
=>x<>pi/12+kpi/2 và x<>pi/4-kpi
Vậy: D=R\{pi/12+kpi/2;pi/4-kpi}
cho sin anpha= 1/3với π<anpha<3π/2 .tính các giá trị lượng giác.
mọi người ơi giúp mình giúp giải bt này với ạ