Cho tam giác ABC với ba đường cao AA', BB', CC'. Gọi H là trực tâm của tam giác đó. Chứng minh rằng :
\(\dfrac{HA'}{AA'}+\dfrac{HB'}{BB'}+\dfrac{HC'}{CC'}=1\)
Ôn tập chương II - Đa giác. Diện tích đa giác
Bài 51 (Sách bài tập - trang 166)
Thảo luận (1)
Bài 52 (Sách bài tập - trang 166)
Cho tam giác ABC
a) Tính tỉ số các đường cao BB' và CC' xuất phát từ các đỉnh B và C
b) Tại sao nếu AB < AC thì BB' < CC'
Thảo luận (1)Hướng dẫn giải
Bài 53 (Sách bài tập - trang 166)
Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thẳng l cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo)
Thảo luận (1)Hướng dẫn giải
Bài 54 (Sách bài tập - trang 166)
Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN ?
Thảo luận (1)Hướng dẫn giải
Bài 55 (Sách bài tập - trang 166)
Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của
a) Các tam giác DAC và DCK
b) Tam giác DAC và tứ giác ADLB
c) Các tứ giác ABKD và ABLD
Thảo luận (1)Hướng dẫn giải
Bài 56 (Sách bài tập - trang 166)
Cho tam giác ABC vuông ở A và có BC = 2 AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG
a) Tính các góc B, C cạnh AC và diện tích tam giác ABC
b) Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE
c) Tính diện tích tứ giác DEFG
Thảo luận (2)Hướng dẫn giải
a) Giả sử M là trung điểm của BC, \(\Delta ABM\) là tam giác đều nên \(\widehat{ABC}=60^o.\)
Từ đó suy ra: \(\widehat{BCA}=30^o\). Theo định lí Py-ta-go, ta có:
AC = \(\sqrt{BC^2-AB^2}\)
AC = \(\sqrt{4a^2-a^2}=a\sqrt{3}.\)
Do đó, ta có:
SABC = \(\dfrac{1}{2}AB.AC=\dfrac{1}{2}a^2\sqrt{3}.\) (1)
b) Vì \(\widehat{FAB}=\widehat{ABC}=60^o\) nên FA // BC (hai góc so le trong), từ đó suy ra FA vuông góc với BE và CG.
Gọi giao điểm của FA và BE là H, giao điểm của FA và CG là K. Ta có:
SFAG = \(\dfrac{1}{2}FA.GK=\dfrac{1}{2}a.\dfrac{a\sqrt{3}}{2}=\dfrac{1}{4}a^2\sqrt{3},\) (2)
SFBE = \(\dfrac{1}{2}BE.FH=\dfrac{1}{2}.2a.\dfrac{a}{2}=\dfrac{1}{2}a^2.\) (3)
c) SBDCE = 4a2, (4)
SABF = \(\dfrac{1}{4}a^2\sqrt{3},\) (5)
SACG = \(\dfrac{3}{4}a^2\sqrt{3}.\) (6)
Từ (1), (2), (3), (4), (5), (6), ta có:
SDEFG = \(\dfrac{a^2}{4}\left(18+7\sqrt{3}\right)\approx7,53a^2.\)
(Trả lời bởi Hải Ngân)
Bài II.1 - Bài tập bổ sung (Sách bài tập - trang 166)
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, D, O. Hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao ?
Thảo luận (2)Hướng dẫn giảiTa có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))
(Trả lời bởi Cheewin)
Bài II.2 - Bài tập bổ sung (Sách bài tập - trang 166)
Cho hình lục giác ABCDEF, có AB = BC = 3cm avf ED = 4cm. Biết rằng ED song song với AB. AB vuông góc với BC, FE vuông góc với FA và FE = FA. Qua điểm A kẻ đường thẳng d song song với BC. Gọi K là giao điểm của d và ED, biết AK = 4cm, KD = 1cm. Tính diện tích của lục giác đó ?
Thảo luận (2)Hướng dẫn giảiGọi H là giao điểm của ED và BC
=> SABHE=\(\dfrac{\left(AB+EH\right).BH}{2}=\dfrac{\left(3+6\right).4}{2}=18\left(cm^2\right)\)
Shình vuông DHC= \(\dfrac{DH.CH}{2}=\dfrac{2.1}{2}=1\left(cm^2\right)\)
Áp dụng định lí Py -ta go trong tam giác vuông EKA
EA=\(\sqrt{EK^2+KA^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
Trong tam giác vuông FEA có FE=FA => \(EF^2=\dfrac{25}{2}\)
=> SFEA=(FE.FA)/2=\(\dfrac{25}{2}:2=\dfrac{25}{4}\left(cm^2\right)\)
vậy S lục giác đã cho = SABHE+ SFEA- Shình vuông DHC=18+\(\dfrac{25}{4}-1=\dfrac{93}{4}\left(cm^2\right)\)
Nhớ tick nha ,đánh quẹo cả tay,em cảm ơn trước ak
(Trả lời bởi Cheewin)
Bài II.3 - Bài tập bổ sung (Sách bài tập - trang 167)
Cho lục giác đều MNPQRS (h.bs.27). Gọi A, Y, Z tương ứng là trung điểm các cạnh MN, PQ và RS. Khi đó XYZ là :
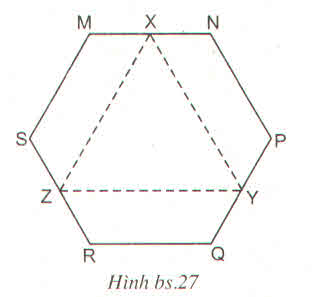
(A) Tam giác vuông
(B) Tam giác vuông cân
(C) Tam giác đều
(D) Tam giác mà độ dài các cạnh của nó đôi một khác nhau
Hãy chọn phương án đúng ?
Thảo luận (1)Hướng dẫn giảiChọn phương án (C): Tam giác đều
(Trả lời bởi Cheewin)
Bài II.4 - Bài tập bổ sung (Sách bài tập - trang 167)
Cho tứ giác MNPQ và các kích thước đã cho trên hình bs.28. Diện tích tam giác MQP bằng bao nhiêu cm^2 ?
(A) 6 (B) 25
(C) dfrac{25}{2} (D) dfrac{25}{4}
Chọn phương án đúng ?
Đọc tiếp
Cho tứ giác MNPQ và các kích thước đã cho trên hình bs.28. Diện tích tam giác MQP bằng bao nhiêu \(cm^2\) ?
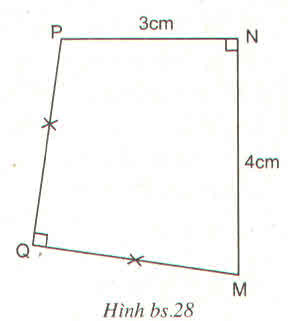
(A) 6 (B) 25
(C) \(\dfrac{25}{2}\) (D) \(\dfrac{25}{4}\)
Chọn phương án đúng ?
Thảo luận (1)Hướng dẫn giảiChọn phương án (D) \(\dfrac{25}{4}\left(cm^2\right)\)
(Trả lời bởi Cheewin)