Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O).
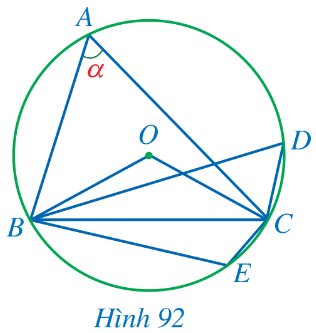
a) Số đo góc BOC là
Α. α. B. 2α. C. 180° – α. D. 180° – 2α.
b) Số đo góc BDC là
Α. α. B. \(\dfrac{\alpha}{2}\). C. 180° – α. D. 180° – \(\dfrac{\alpha}{2}\).
c) Số đo góc BEC là
Α. α. B. 2α. C. 180° – α. D. 360° – α.