a)
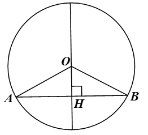
Gọi (O) là đường tròn có đường kính vuông góc với dây AB tại H.
Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.
∆OAB cân tại O có OH là đường cao (do OH ⊥ AB) nên đồng thời là đường trung tuyến của tam giác. Do đó H là trung điểm của AB.
Vậy đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
b)
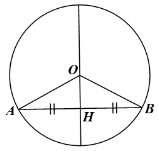
Gọi (O) là đường tròn có đường kính đi qua trung điểm H của dây AB.
Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.
∆OAB cân tại O có OH là đường trung tuyến nên đồng thời là đường cao của tam giác. Do đó OH ⊥ AB tại H.
Vậy đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
c)
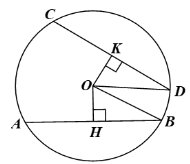
Gọi \(OH,OK\)lần lượt là khoảng cách từ \(O\) tới \(AB,CD\).
Do \(AB = CD \Rightarrow AH = CK\).
Xét tam giác \(OAH\) và tam giác \(OCK\) có:
\(\widehat {AHO} = \widehat {CKO} = 90^\circ \)
\(OA = OC = R\)
\(AH = CK\)
\( \Rightarrow \Delta AHO = \Delta CKO\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow OH = OK\) (cạnh tương ứng).
d)
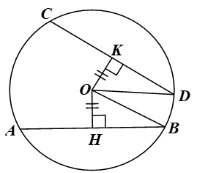
Gọi $(\mathrm{O})$ là đường tròn có hai dây $\mathrm{AB}, \mathrm{CD}$ bằng nhau. $\mathrm{Gọi} \mathrm{OH}, \mathrm{OK}$ lần lượt là khoảng cách từ O đến AB , CD . Khi đó $\mathrm{OH} \perp \mathrm{AB}$ tại $\mathrm{H}, \mathrm{OK} \perp \mathrm{CD}$ tại K .
Do đó, theo kết quả của câu a, ta có: $H, K$ lần lượt là trung điểm của $A B, C D$.
Suy ra $A B=2 \mathrm{HB}$ và $C D=2 \mathrm{KD}$.
Theo bài, $\mathrm{OH}=\mathrm{OK}$, suy ra $\mathrm{OH}^2=\mathrm{OK}^2$. (1)
Xét $\triangle \mathrm{OHB}$ vuông tại H , ta có: $\mathrm{OB}^2=\mathrm{OH}^2+\mathrm{HB}^2$ (định lí Pythagore).
Suy ra $\mathrm{HB}^2=\mathrm{OB}^2-\mathrm{OH}^2=\mathrm{R}^2-\mathrm{OH}^2$. (2)
Xét $\triangle O K D$ vuông tại H , ta có: $O D^2=O K^2+K D^2$ (định lí Pythagore).
Suy ra $K D^2=O D^2-O K^2=R^2-O K^2$. (3)
Từ (1), (2) và (3) suy ra $\mathrm{HB}^2=K D^2$, hay $\mathrm{HB}=\mathrm{KD}$.
Do đó $2 \mathrm{HB}=2 \mathrm{KD}$ hay $\mathrm{AB}=\mathrm{CD}$.
Vậy hai dây cách đều tâm thì bằng nhau.


