Trong Ví dụ 3, hãy tính độ dài của vectơ \(\overrightarrow {AC} + \overrightarrow {C'D'} \).
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).
Bài 6. Vectơ trong không gian
Luyện tập 3 (SGK Kết nối tri thức với cuộc sống trang 50)
Thảo luận (1)
Luyện tập 4 (SGK Kết nối tri thức với cuộc sống trang 50)
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
Thảo luận (1)Hướng dẫn giảiTa có: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {BD} } \right)\)
\( = \overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {DD} = \overrightarrow {AD} + \overrightarrow {CB} \) (đpcm)
(Trả lời bởi Hà Quang Minh)
Câu hỏi (SGK Kết nối tri thức với cuộc sống trang 47)
Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?
Thảo luận (1)Hướng dẫn giảiGiả sử có ba vectơ \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) sao cho: \(\overrightarrow a = \overrightarrow b \) và \(\overrightarrow b = \overrightarrow c \).
Vì \(\overrightarrow a = \overrightarrow b \) nên hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\) (1)
Vì \(\overrightarrow b = \overrightarrow c \) nên hai vectơ \(\overrightarrow c \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow c } \right| = \left| {\overrightarrow b } \right|\) (2)
Từ (1) và (2) ta có hai vectơ \(\overrightarrow a \), \(\overrightarrow c \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow c } \right|\). Do đó, \(\overrightarrow a = \overrightarrow c \)
Do đó, hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó bằng nhau.
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (SGK Kết nối tri thức với cuộc sống trang 49)
Trong không gian, cho hai vectơ overrightarrow a và overrightarrow b không cùng phương. Lấy điểm A và vẽ các vectơ overrightarrow {AB} overrightarrow a ,overrightarrow {BC} overrightarrow b . Lấy điểm A’ và vẽ các vectơ overrightarrow {AB} overrightarrow a ,overrightarrow {BC} overrightarrow b (H.2.10).a) Giải thích vì sao overrightarrow {AA} overrightarrow {BB} và overrightarrow {BB} overrightarrow {CC} .b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra overrightarrow...
Đọc tiếp
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Lấy điểm A và vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ và vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\overrightarrow {B'C'} = \overrightarrow b \) (H.2.10).
a) Giải thích vì sao \(\overrightarrow {AA'} = \overrightarrow {BB'} \) và \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Thảo luận (1)Hướng dẫn giảia) Vì \(\overrightarrow {AB} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {A'B'} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {A'B'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {A'B'} \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và \(AB = A'B'\). Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và \(AA' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \).
Vì \(\overrightarrow {BC} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {BC} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {B'C'} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và \(BC = B'C'\). Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và \(CC' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Vì hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài; hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và \(AA' = CC'\) nên tứ giác AA’C’C là hình bình hành. Suy ra, \(AC = A'C'\) và AC//A’C’. Do đó, hai vectơ \(\overrightarrow {AC} ,\overrightarrow {A'C'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
(Trả lời bởi Hà Quang Minh)
Luyện tập 2 (SGK Kết nối tri thức với cuộc sống trang 48)
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.
a) Trong ba vectơ \(\overrightarrow {SC} ,\overrightarrow {AD} \) và \(\overrightarrow {DC} \), vectơ nào bằng vectơ \(\overrightarrow {AB} \).
b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm N sao cho \(\overrightarrow {MN} = \overrightarrow {AB} \).
Thảo luận (1)Hướng dẫn giảia) Vì ABCD là hình bình hành nên AB//CD và \(AB = CD\). Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.
Vì AB và SC chéo nhau nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không cùng phương. Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không bằng nhau.
Vì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không cùng phương nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không bằng nhau.
b) Qua M vẽ đường thẳng song song với AB cắt BC tại N.
Tứ giác ABNM có: AB//MN, AM//BN nên tứ giác ABNM là hình bình hành. Do đó, \(AB = MN\), lại có: AB//MN nên hai vectơ \(\overrightarrow {MN} ,\overrightarrow {AB} \) cùng độ dài và cùng hướng. Suy ra, \(\overrightarrow {MN} = \overrightarrow {AB} \). Vậy điểm N cần tìm là giao điểm của đường thẳng qua M song song với AB và cạnh BC.
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống trang 47)
Cho hình hộp ABCD.A’B’C’D’ (H.2.7)a) So sánh độ dài hai vectơ overrightarrow {AB} và overrightarrow {DC} .b) Nhận xét về giá của hai vectơ overrightarrow {AB} và overrightarrow {DC} .c) Hai vectơ overrightarrow {AB} và overrightarrow {DC} có cùng phương không? Có cùng hướng không?
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ (H.2.7)
a) So sánh độ dài hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
b) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) có cùng phương không? Có cùng hướng không?
Thảo luận (1)Hướng dẫn giảia) Vì ABCD.A’B’C’D’ là hình hộp nên ABCD và DCC’D’ là các hình bình hành. Suy ra, \(AB = CD = D'C'\). Do đó, \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {D'C'} } \right|\).
b) Vì ABCD và DCC’D’ là các hình bình hành nên AB//CD, CD//C’D’. Do đó, AB//C’D’. Vậy giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) song song với nhau.
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) cùng phương và cùng hướng.
(Trả lời bởi Hà Quang Minh)
Câu hỏi (SGK Kết nối tri thức với cuộc sống trang 6)
Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.
Thảo luận (1)Hướng dẫn giảiMột số ví dụ khác:
a) Hướng bay của khinh khí cầu:
b) Hướng đi của thuyền trên sông:
(Trả lời bởi Hà Quang Minh)
Hoạt động 1 (SGK Kết nối tri thức với cuộc sống trang 46)
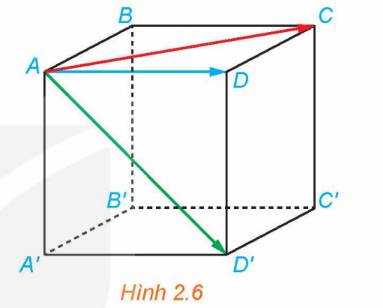
Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.
a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các các lực căng dây?
b) Các đoạn thẳng này có cùng nằm trong một mặt phẳng không?
Thảo luận (1)Hướng dẫn giảia) Các đoạn thẳng này có hướng lên trên (về phía móc cần cẩu) và độ dài của các đoạn thẳng thể hiện cho độ lớn của các lực căng dây và được lấy tỉ lệ với độ lớn của các lực căng dây.
b) Các đoạn thẳng này không cùng nằm trên một mặt phẳng.
(Trả lời bởi Hà Quang Minh)
Luyện tập 1 (SGK Kết nối tri thức với cuộc sống trang 47)
Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \):
a) Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)?
b) Hai vectơ nào có cùng độ dài?
Thảo luận (1)Hướng dẫn giảia) Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \), hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} \) có giá nằm trong mặt phẳng (ABCD)
b) Vì ABCD.A’B’C’D’ là hình lập phương nên \(AD = DC = DD'\)
Tam giác ADD’ vuông tại D nên theo định lý Pythagore ta có:
\(AD' = \sqrt {A{D^2} + DD{'^2}} = AD\sqrt 2 \)
Tam giác ADC vuông tại D nên theo định lý Pythagore ta có:
\(AC = \sqrt {A{D^2} + D{C^2}} = AD\sqrt 2 \)
Do đó, \(AD' = AC\) hay \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD'} } \right|\). Vậy hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD'} \) có cùng độ dài.
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (SGK Kết nối tri thức với cuộc sống trang 48)
Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.
Thảo luận (1)Hướng dẫn giảiGọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 của tòa nhà là \(\overrightarrow a \). Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 22 lên tầng 29 của tòa nhà là \(\overrightarrow b \).
Vì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều dịch chuyển từ tầng thấp lên tầng cao nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có cùng hướng (1).
Độ dài vectơ \(\overrightarrow a \) là: \(\left| {\overrightarrow a } \right| = 7\), độ dài vectơ \(\overrightarrow b \) là: \(\left| {\overrightarrow b } \right| = 7\) nên \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 7\) (2)
Từ (1) và (2) ta có: \(\overrightarrow a = \overrightarrow b \). Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau.
(Trả lời bởi Hà Quang Minh)