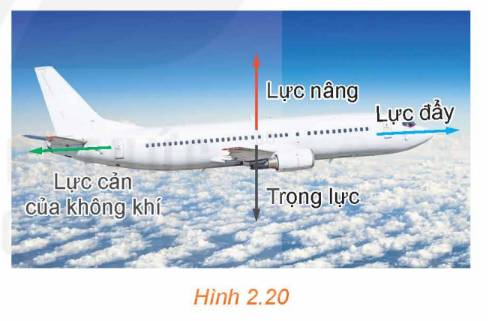
Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900km/h lên 920km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900km/h và 920km/h lần lượt được biểu diễn bởi hai vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \). Hãy giải thích vì sao \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).