Bài 6. Vectơ trong không gian

Hướng dẫn giải

Giả sử có ba vectơ \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) sao cho: \(\overrightarrow a  = \overrightarrow b \) và \(\overrightarrow b  = \overrightarrow c \).

Vì \(\overrightarrow a  = \overrightarrow b \) nên hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\) (1)

Vì \(\overrightarrow b  = \overrightarrow c \) nên hai vectơ \(\overrightarrow c \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow c } \right| = \left| {\overrightarrow b } \right|\) (2)

Từ (1) và (2) ta có hai vectơ \(\overrightarrow a \), \(\overrightarrow c \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow c } \right|\). Do đó, \(\overrightarrow a  = \overrightarrow c \)

Do đó, hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó bằng nhau.

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Góc giữa hai vectơ cùng hướng bằng \({0^0}\).

Góc giữa hai vectơ ngược hướng bằng \({180^0}\).

(Trả lời bởi Hà Quang Minh)

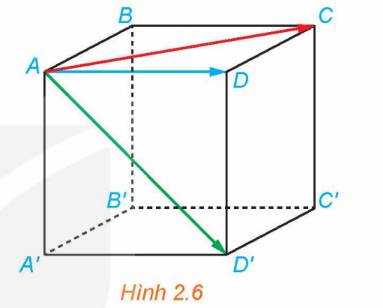
Hướng dẫn giải

a) Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \), hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} \) có giá nằm trong mặt phẳng (ABCD)

b) Vì ABCD.A’B’C’D’ là hình lập phương nên \(AD = DC = DD'\)

Tam giác ADD’ vuông tại D nên theo định lý Pythagore ta có:

\(AD' = \sqrt {A{D^2} + DD{'^2}}  = AD\sqrt 2 \)

Tam giác ADC vuông tại D nên theo định lý Pythagore ta có:

\(AC = \sqrt {A{D^2} + D{C^2}}  = AD\sqrt 2 \)

 Do đó, \(AD' = AC\) hay \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD'} } \right|\). Vậy hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD'} \) có cùng độ dài.

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Giá của các vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {AE} \) cùng nằm trên mặt phẳng (ACDE). (1)

Vì DCAE là hình bình hành nên \(\overrightarrow {AC}  + \overrightarrow {AE}  = \overrightarrow {AD} \) (quy tắc hình bình hành)

Vì các lực kéo làm cho ba sợi dây ở trạng thái đứng yên nên \(\overrightarrow {AD}  =  - \overrightarrow {AB} \), do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {AB} \) có giá cùng nằm trên một mặt phẳng (ACDE). (2)

Từ (1) và (2) suy ra ba vectơ \(\overrightarrow {AC} \), \(\overrightarrow {AE} \) và \(\overrightarrow {AB} \) có giá cùng nằm trên mặt phẳng (ACDE).

Vậy khi các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng

(Trả lời bởi Hà Quang Minh)

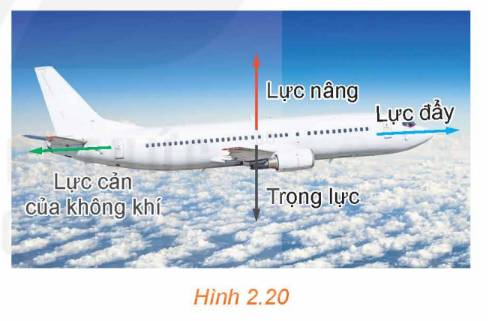
Hướng dẫn giải

Vì trong quá trình máy bay tăng vận tốc từ 900km/h lên 920km/h máy bay giữ nguyên hướng bay nên vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có cùng hướng. Do đó, \(\overrightarrow {{F_1}}  = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó (1).

Gọi \({v_1},{v_2}\) lần lượt là vận tốc của của chiếc máy bay khi đạt 900km/h và 920km/h.

Suy ra \({v_1} = 900\left( {km/h} \right),{v_2} = 920\left( {km/h} \right)\)

Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên

\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{\left| {\overrightarrow {{F_2}} } \right|}} = \frac{{v_1^2}}{{v_2^2}} = \frac{{{{900}^2}}}{{{{920}^2}}} = \frac{{2025}}{{2116}} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \frac{{2025}}{{2116}}\left| {\overrightarrow {{F_2}} } \right|\) (2)

Từ (1) và (2) ta có: \(\overrightarrow {{F_1}}  = \frac{{2025}}{{2116}}\overrightarrow {{F_2}}  \Rightarrow k = \frac{{2025}}{{2116}} \approx 0,96\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a) Ta có: \(\overrightarrow {AC} .\overrightarrow {CD}  + \overrightarrow {BC} .\overrightarrow {DC}  = \overrightarrow {AC} .\overrightarrow {CD}  - \overrightarrow {BC} .\overrightarrow {CD}  = \overrightarrow {CD} \left( {\overrightarrow {AC}  + \overrightarrow {CB} } \right) = \overrightarrow {CD} .\overrightarrow {AB} \) (đpcm)

b) \(\overrightarrow {AB} .\overrightarrow {CD}  + \overrightarrow {AC} .\overrightarrow {DB}  + \overrightarrow {AD} .\overrightarrow {BC}  = \overrightarrow {AB} .\overrightarrow {CD}  + \left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right).\overrightarrow {DB}  + \left( {\overrightarrow {AB}  + \overrightarrow {BD} } \right).\overrightarrow {BC} \)

\( = \overrightarrow {AB} .\overrightarrow {CD}  + \overrightarrow {AB} .\overrightarrow {DB}  + \overrightarrow {BC} .\overrightarrow {DB}  + \overrightarrow {AB} .\overrightarrow {BC}  + \overrightarrow {BD} .\overrightarrow {BC} \)

\( = \overrightarrow {AB} .\left( {\overrightarrow {CD}  + \overrightarrow {DB}  + \overrightarrow {BC} } \right) + \left( {\overrightarrow {BC} .\overrightarrow {DB}  + \overrightarrow {BD} .\overrightarrow {BC} } \right) = \overrightarrow {AB} .\left( {\overrightarrow {CB}  + \overrightarrow {BC} } \right) + \overrightarrow {BC} \left( {\overrightarrow {DB}  + \overrightarrow {BD} } \right) = 0\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a) Vì AA’//CC’ nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {C'C} \) ngược hướng nhau.

Suy ra, \(\left( {\overrightarrow {AA'} ,\overrightarrow {C'C} } \right) = {180^0}\).

Do đó, \(\overrightarrow {AA'} .\overrightarrow {C'C}  = \left| {\overrightarrow {AA'} } \right|.\left| {\overrightarrow {C'C} } \right|.\cos \left( {\overrightarrow {AA'} ,\overrightarrow {C'C} } \right) = 2.2.\cos {180^0} =  - 4\)

b) Vì A’ADD’ là hình chữ nhật nên \(\widehat {A'AD} = {90^0}\)

Vì ABCD là hình vuông nên \(\overrightarrow {BC}  = \overrightarrow {AD} \). Do đó, \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AA'} ,\overrightarrow {AD} } \right) = \widehat {A'AD} = {90^0}\)

Ta có: \(\overrightarrow {AA'} .\overrightarrow {BC}  = \overrightarrow {AA'} .\overrightarrow {AD}  = \left| {\overrightarrow {AA'} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AA'} ,\overrightarrow {AD} } \right) = 2.1.\cos {90^0} = 0\)

c) Vì A’ABB’ là hình chữ nhật nên \(\overrightarrow {B'A'}  = \overrightarrow {BA} \).

Vì ABCD là hình vuông nên \(\widehat {CAB} = {45^0}\) và \(AC = \sqrt 2 \)

Ta có: \(\overrightarrow {AC} .\overrightarrow {B'A'}  =  - \overrightarrow {AC} .\overrightarrow {AB}  =  - \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AB} } \right) =  - \sqrt 2 .1.\cos {45^0} =  - 1\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Chứng minh: Nếu tứ giác ABCD là hình bình hành thì \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \)

Gọi O là tâm hình bình hành ABCD. Khi đó, O là trung điểm của AC, BD.

Suy ra \(\overrightarrow {OC}  =  - \overrightarrow {OA} ,\overrightarrow {OD}  =  - \overrightarrow {OB} \)

Ta có: \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SO}  + \overrightarrow {OA}  + \overrightarrow {SO}  + \overrightarrow {OC}  = 2\overrightarrow {SO}  + \left( {\overrightarrow {OA}  - \overrightarrow {OA} } \right) = 2\overrightarrow {SO} \)

\(\overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SO}  + \overrightarrow {OB}  + \overrightarrow {SO}  + \overrightarrow {OD}  = 2\overrightarrow {SO}  + \left( {\overrightarrow {OB}  - \overrightarrow {OB} } \right) = 2\overrightarrow {SO} \)

Do đó, \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \)

Chứng minh: Nếu \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \) thì tứ giác ABCD là hình bình hành:

Ta có: \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD}  \Leftrightarrow \overrightarrow {SA}  - \overrightarrow {SB}  = \overrightarrow {SD}  - \overrightarrow {SC}  \Leftrightarrow \overrightarrow {BA}  = \overrightarrow {CD} \)

Suy ra, hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng hướng và có độ lớn bằng nhau.

Suy ra, \(AB = CD,\) AB//CD. Khi đó, tứ giác ABCD là hình bình hành.

Vậy tứ giác ABCD là hình bình hành nếu và chỉ nếu \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Gọi O là giao điểm của hai đường chéo AC và BD trong hình vuông ABCD. Do đó, O là trung điểm của BD, O là trung điểm của AC.

Tứ giác ABCD là hình vuông cạnh a nên độ dài đường chéo BD là \(a\sqrt 2 \)\( \Rightarrow OB = \frac{{a\sqrt 2 }}{2}\)

Gọi E là trung điểm của SC. Mà O là trung điểm của AC nên OE là đường trung bình của tam giác SAC, do đó, OE//SA, \(OE = \frac{1}{2}SA = \frac{a}{2}\). Suy ra: \(\overrightarrow {AS}  = 2\overrightarrow {OE} \)

Vì O là trung điểm của BD nên \(\overrightarrow {BD}  = 2\overrightarrow {OB} \)

Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, BE là đường trung tuyến đồng thời là đường cao của tam giác SBC. Do đó, \(EB = \frac{{a\sqrt 3 }}{2}\).

Ta có: \(O{E^2} + O{B^2} = \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{3{a^2}}}{4} = E{B^2}\) nên \(\Delta \)EOB vuông tại O. Do đó, \(\overrightarrow {OE}  \bot \overrightarrow {OB} \)

Ta có: \(\overrightarrow {AS} .\overrightarrow {BD}  = 2\overrightarrow {OE} .\left( { - 2\overrightarrow {OB} } \right) =  - 4\overrightarrow {OE} .\overrightarrow {OB}  = 0\)

Tứ giác ABCD là hình vuông nên \(\overrightarrow {CD}  = \overrightarrow {BA} \)

Ta có: \(\overrightarrow {AS} .\overrightarrow {CD}  = \overrightarrow {AS} .\overrightarrow {BA}  =  - \overrightarrow {AS} .\overrightarrow {AB}  =  - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \left( {\overrightarrow {AS} ,\overrightarrow {AB} } \right) =  - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB}\)

Vì tam giác SAB có ba cạnh bằng nhau nên tam giác SAB đều, suy ra \(\widehat {SAB} = {60^0}\)

Suy ra: \(\overrightarrow {AS} .\overrightarrow {CD}  =  - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB} =  - a.a.\cos {60^0} = \frac{{ - {a^2}}}{2}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Ta có: \(\overrightarrow {AB}  + \overrightarrow {CD}  = \overrightarrow {AD}  + \overrightarrow {DB}  + \overrightarrow {CB}  + \overrightarrow {BD}  = \left( {\overrightarrow {AD}  + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB}  + \overrightarrow {BD} } \right)\)

\( = \overrightarrow {AD}  + \overrightarrow {CB}  + \overrightarrow {DD}  = \overrightarrow {AD}  + \overrightarrow {CB} \) (đpcm)

(Trả lời bởi Hà Quang Minh)