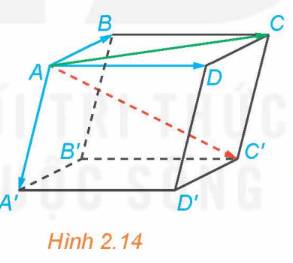
Cho hình hộp ABCD.A’B’C’D’ (H.2.14).
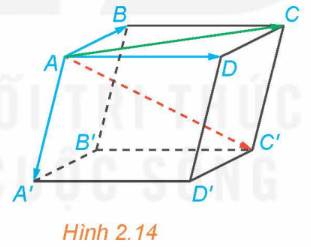
a) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
Thảo luận (1)Hướng dẫn giảiQuy tắc hình hộp với các vectơ có điểm đầu là B là: \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
(Trả lời bởi Hà Quang Minh)
Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BD'} \).
Thảo luận (1)Hướng dẫn giảiVì ABCD là hình chữ nhật nên \(\overrightarrow {AD} = \overrightarrow {BC} ,\overrightarrow {CD} = \overrightarrow {BA} \)
Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên \(\overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Ta có: \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
(Trả lời bởi Hà Quang Minh)
Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.
Thảo luận (1)Hướng dẫn giảiCác vectơ biểu diễn hai lực đó có độ dài bằng nhau và hướng của chúng là ngược nhau.
(Trả lời bởi Hà Quang Minh)
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SC} \)
Thảo luận (1)Hướng dẫn giảia) Tứ giác ABCD là hình bình hành nên \(AB = CD\), AB//CD. Suy ra \(BM = DN\) (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, \(BN = DM\) và BN//DM. Hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) có cùng độ dài và ngược hướng nên \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau.
b) Theo a ta có: \(\overrightarrow {BN} = - \overrightarrow {DM} \)
Do đó, \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SD} + \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {SM} + \overrightarrow {MC} = \overrightarrow {SC} \)
(Trả lời bởi Hà Quang Minh)
Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.
Thảo luận (1)Hướng dẫn giảiVectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.
(Trả lời bởi Hà Quang Minh)
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)
a) Hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương không? Có cùng hướng không?
b) Giải thích vì sao \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
Thảo luận (1)Hướng dẫn giảia) Vì MN là đường trung bình của tam giác ABC nên MN//BC.
Vì BCC’B’ là hình bình hành nên BC//B’C’. Suy ra: MN//B’C’.
Do đó hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương và cùng hướng.
b) Vì BCC’B’ là hình bình hành nên \(BC = B'C'\)
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}BC\)
Suy ra: \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
(Trả lời bởi Hà Quang Minh)
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau không? Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) có bằng nhau không?
Thảo luận (1)Hướng dẫn giảiHai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) bằng nhau vì chúng có cùng độ dài và cùng hướng.
Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) bằng nhau chúng có cùng độ dài và cùng hướng.
(Trả lời bởi Hà Quang Minh)
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
Thảo luận (1)Hướng dẫn giảiVì \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB \Rightarrow \frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\left( { = \frac{1}{3}} \right)\)
Tam giác SAB có: \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\) nên FE//AB và \(EF = \frac{1}{3}AB\).
Vì hai vectơ \(\overrightarrow {EF} \) và \(\overrightarrow {AB} \) cùng hướng nên \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AB} \) (1)
Vì ABCD là hình bình hành nên \(AB = CD\) và AB//CD. Do đó, \(\overrightarrow {AB} = \overrightarrow {DC} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \)
(Trả lời bởi Hà Quang Minh)
Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho \(\overrightarrow {AI} = 3\overrightarrow {IG} \) (H.2.19). Chứng minh rằng \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
Thảo luận (1)Hướng dẫn giảiTheo ví dụ 8 ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \)\( \Rightarrow \overrightarrow {AI} + \overrightarrow {IB} + \overrightarrow {AI} + \overrightarrow {IC} + \overrightarrow {AI} + \overrightarrow {ID} = 3\overrightarrow {AG} \)
\( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 3\overrightarrow {AG} - 3\overrightarrow {AI} = 3\left( {\overrightarrow {AG} + \overrightarrow {IA} } \right) = 3\overrightarrow {IG} = \overrightarrow {AI} \)\( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \)
(Trả lời bởi Hà Quang Minh)