Cho hình hộp ABCD.A’B’C’D’ (H.2.7)
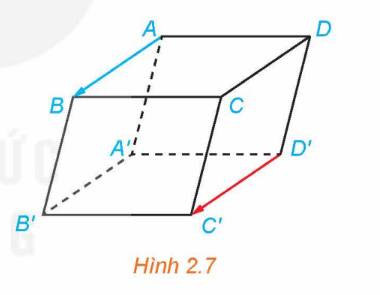
a) So sánh độ dài hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
b) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) có cùng phương không? Có cùng hướng không?
a) Vì ABCD.A’B’C’D’ là hình hộp nên ABCD và DCC’D’ là các hình bình hành. Suy ra, \(AB = CD = D'C'\). Do đó, \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {D'C'} } \right|\).
b) Vì ABCD và DCC’D’ là các hình bình hành nên AB//CD, CD//C’D’. Do đó, AB//C’D’. Vậy giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) song song với nhau.
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) cùng phương và cùng hướng.




